As soon as I wrote it, I realized that the title is much more general than anything that can be fit in a blog post. Bekenstein argued long ago that the missing mass problem should instead be called the acceleration discrepancy, because that’s what it is – a discrepancy that occurs in conventional dynamics at a particular acceleration scale. So in that sense, it is the entire history of dark matter. For that, I recommend the excellent book The Dark Matter Problem: A Historical Perspective by Bob Sanders.
Here I mean more specifically my own attempts to empirically constrain the relation between the mass discrepancy and acceleration. Milgrom introduced MOND in 1983, no doubt after a long period of development and refereeing. He anticipated essentially all of what I’m going to describe. But not everyone is eager to accept MOND as a new fundamental theory, and often suffer from a very human tendency to confuse fact and theory. So I have gone out of my way to demonstrate what is empirically true in the data – facts – irrespective of theoretical interpretation (MOND or otherwise).
What is empirically true, and now observationally established beyond a reasonable doubt, is that the mass discrepancy in rotating galaxies correlates with centripetal acceleration. The lower the acceleration, the more dark matter one appears to need. Or, as Bekenstein might have put it, the amplitude of the acceleration discrepancy grows as the acceleration itself declines.
Bob Sanders made the first empirical demonstration that I am aware of that the mass discrepancy correlates with acceleration. In a wide ranging and still relevant 1990 review, he showed that the amplitude of the mass discrepancy correlated with the acceleration at the last measured point of a rotation curve. It did not correlate with radius.

I was completely unaware of this when I became interested in the problem a few years later. I wound up reinventing the very same term – the mass discrepancy, which I defined as the ratio of dynamically measured mass to that visible in baryons: D = Mtot/Mbar. When there is no dark matter, Mtot = Mbar and D = 1.
My first demonstration of this effect was presented at a conference at Rutgers in 1998. This considered the mass discrepancy at every radius and every acceleration within all the galaxies that were available to me at that time. Though messy, as is often the case in extragalactic astronomy, the correlation was clear. Indeed, this was part of a broader review of galaxy formation; the title, abstract, and much of the substance remains relevant today.

I spent much of the following five years collecting more data, refining the analysis, and sweating the details of uncertainties and systematic instrumental effects. In 2004, I published an extended and improved version, now with over 5 dozen galaxies.

Here I’ve used a population synthesis model to estimate the mass-to-light ratio of the stars. This is the only unknown; everything else is measured. Note that the vast majority galaxies land on top of each other. There are a few that do not, as you can perceive in the parallel sets of points offset from the main body. But that happens in only a few cases, as expected – no population model is perfect. Indeed, this one was surprisingly good, as the vast majority of the individual galaxies are indistinguishable in the pile that defines the main relation.
I explored the how the estimation of the stellar mass-to-light ratio affected this mass discrepancy-acceleration relation in great detail in the 2004 paper. The details differ with the choice of estimator, but the bottom line was that the relation persisted for any plausible choice. The relation exists. It is an empirical fact.
At this juncture, further improvement was no longer limited by rotation curve data, which is what we had been working to expand through the early ’00s. Now it was the stellar mass. The measurement of stellar mass was based on optical measurements of the luminosity distribution of stars in galaxies. These are perfectly fine data, but it is hard to map the starlight that we measured to the stellar mass that we need for this relation. The population synthesis models were good, but they weren’t good enough to avoid the occasional outlier, as can be seen in the figure above.
One thing the models all agreed on (before they didn’t, then they did again) was that the near-infrared would provide a more robust way of mapping stellar mass than the optical bands we had been using up till then. This was the clear way forward, and perhaps the only hope for improving the data further. Fortunately, technology was keeping pace. Around this time, I became involved in helping the effort to develop the NEWFIRM near-infrared camera for the national observatories, and NASA had just launched the Spitzer space telescope. These were the right tools in the right place at the right time. Ultimately, the high accuracy of the deep images obtained from the dark of space by Spitzer at 3.6 microns were to prove most valuable.
Jim Schombert and I spent much of the following decade observing in the near-infrared. Many other observers were doing this as well, filling the Spitzer archive with useful data while we concentrated on our own list of low surface brightness galaxies. This paragraph cannot suffice to convey the long term effort and enormity of this program. But by the mid-teens, we had accumulated data for hundreds of galaxies, including all those for which we also had rotation curves and HI observations. The latter had been obtained over the course of decades by an entire independent community of radio observers, and represent an integrated effort that dwarfs our own.
On top of the observational effort, Jim had been busy building updated stellar population models. We have a sophisticated understanding of how stars work, but things can get complicated when you put billions of them together. Nevertheless, Jim’s work – and that of a number of independent workers – indicated that the relation between Spitzer’s 3.6 micron luminosity measurements and stellar mass should be remarkably simple – basically just a constant conversion factor for nearly all star forming galaxies like those in our sample.
Things came together when Federico Lelli joined Case Western as a postdoc in 2014. He had completed his Ph.D. in the rich tradition of radio astronomy, and was the perfect person to move the project forward. After a couple more years of effort, curating the rotation curve data and building mass models from the Spitzer data, we were in the position to build the relation for over a dozen dozen galaxies. With all the hard work done, making the plot was a matter of running a pre-prepared computer script.
Federico ran his script. The plot appeared on his screen. In a stunned voice, he called me into his office. We had expected an improvement with the Spitzer data – hence the decade of work – but we had also expected there to be a few outliers. There weren’t. Any.
All. the. galaxies. fell. right. on. top. of. each. other.
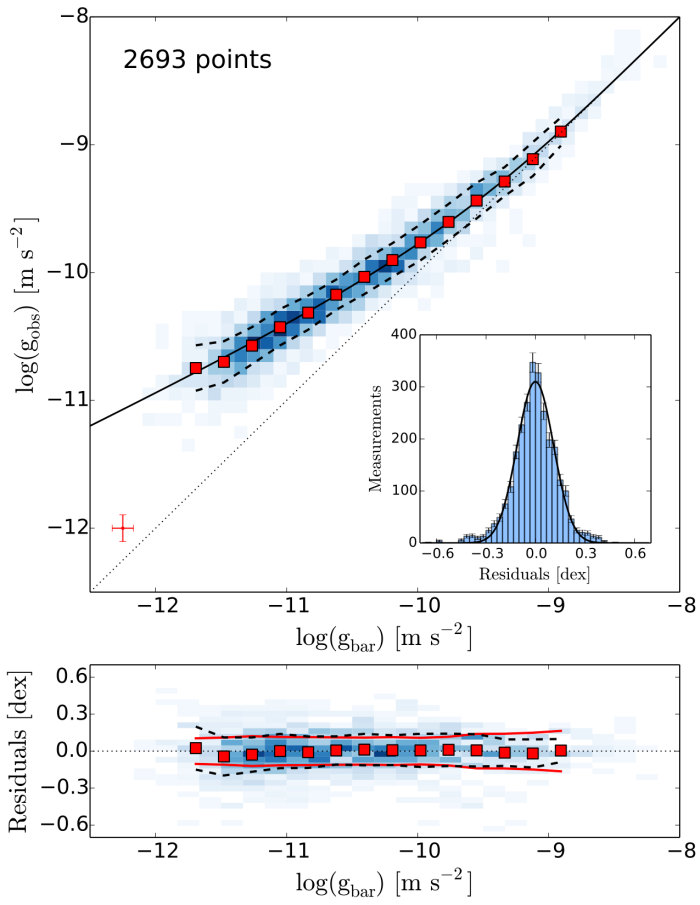
This plot differs from those above because we had decided to plot the measured acceleration against that predicted by the observed baryons so that the two axes would be independent. The discrepancy, defined as the ratio, depended on both. D is essentially the ratio of the y-axis to the x-axis of this last plot, dividing out the unity slope where D = 1.
This was one of the most satisfactory moments of my long career, in which I have been fortunate to have had many satisfactory moments. It is right up there with the eureka moment I had that finally broke the long-standing loggerhead about the role of selection effects in Freeman’s Law. (Young astronomers – never heard of Freeman’s Law? You’re welcome.) Or the epiphany that, gee, maybe what we’re calling dark matter could be a proxy for something deeper. It was also gratifying that it was quickly recognized as such, with many of the colleagues I first presented it to saying it was the highlight of the conference where it was first unveiled.
Regardless of the ultimate interpretation of the radial acceleration relation, it clearly exists in the data for rotating galaxies. The discrepancy appears at a characteristic acceleration scale, g† = 1.2 x 10-10 m/s/s. That number is in the data. Why? is a deeply profound question.
It isn’t just that the acceleration scale is somehow fundamental. The amplitude of the discrepancy depends systematically on the acceleration. Above the critical scale, all is well: no need for dark matter. Below it, the amplitude of the discrepancy – the amount of dark matter we infer – increases systematically. The lower the acceleration, the more dark matter one infers.
The relation for rotating galaxies has no detectable scatter – it is a near-perfect relation. Whether this persists, and holds for other systems, is the interesting outstanding question. It appears, for example, that dwarf spheroidal galaxies may follow a slightly different relation. However, the emphasis here is on slighlty. Very few of these data pass the same quality criteria that the SPARC data plotted above do. It’s like comparing mud pies with diamonds.
Whether the scatter in the radial acceleration relation is zero or merely very tiny is important. That’s the difference between a new fundamental force law (like MOND) and a merely spectacular galaxy scaling relation. For this reason, it seems to be controversial. It shouldn’t be: I was surprised at how tight the relation was myself. But I don’t get to report that there is lots of scatter when there isn’t. To do so would be profoundly unscientific, regardless of the wants of the crowd.
Of course, science is hard. If you don’t do everything right, from the measurements to the mass models to the stellar populations, you’ll find some scatter where perhaps there isn’t any. There are so many creative ways to screw up that I’m sure people will continue to find them. Myself, I prefer to look forward: I see no need to continuously re-establish what has been repeatedly demonstrated in the history briefly outlined above.
btw
Ethan Siegel directly addresses you and sabine august 2018 scientifc american article here
https://www.forbes.com/sites/startswithabang/2018/07/26/theres-a-debate-raging-over-whether-dark-matter-is-real-but-one-side-is-cheating/#36598d1a7ae4
tl;dr there’s no debate, dark matter is real
LikeLike
Daniel, Ethan Siegel’s use of “cheating” is ridiculous and bordering on offensive. Stacy is intellectually honest to the extreme. He exemplifies the best qualities that Feynman discusses in his famous “Cargo Cult Science” address, and he has always been up front about the strengths and weaknesses of both MOND and LCDM. I unfortunately cannot say the same about some of those who are convinced 100% that dark matter *must* be real.
LikeLiked by 3 people
Thanks. I do try.
LikeLiked by 1 person
“cheating” is a strong word. but it’s one of those rare times when Ethan Siegel DIRECTLY addreses Sabine Hossfelder and Stacy Mcgaugh.
Is there a reason MOND and dark matter in the form of (primordial) black holes, or possibly neutrinos, couldn’t both be correct? so MOND explains galaxy rotation curves, and the dark matter is all black holes, (or possibly neutrinos) which also explains CMB and large scale structure? maybe there’s more neutrinos than standard big bang cosmology, and more black holes.
maybe the big bang has to be adjusted to explain (primordial) black holes, but there’s no agreement on inflation either.
to put it another way, what if i want to create a model a simulation of MOND + black holes and (possibly) more neutrinos, how would such a universe look in comparison to the real universe.
LikeLike
Just to appreciate some of the tactics used by Ethan Siegel, see :
https://darkmattercrisis.wordpress.com/category/science-communication/
Best and thahks for this blog,
Norbert
LikeLiked by 1 person
@Daniel I have been searching for Ethan Siegal’s recent peer reviewed papers on the subjects he blogs about such galaxy rotation curves dark energy and dark matter and I found nada,zilch and zero. I would not count his opinion as coming from an expert but from a commentator.
LikeLike
Daniel;
Regardless of his credentials, Siegel’s essay settles only the question of which side of the debate Siegel is on.
The discrepancy that led to this debate is quite real.
DM v. MOND v. Something Else remains very much unsettled.
sean s.
LikeLike
If dark matter is real, where is it? Show me a piece already. That is not an unreasonable expectation at this juncture in the history of science.
If WIMPs are the dark matter, we should have found them already. The people who express supreme confidence in the existence of dark matter have, for the past several decades, been equally confident that it had to be WIMPs. I am skeptical of their overconfidence.
If we detect dark matter, great: then we know. If we continue not to detect it, we continue only to know what doesn’t work.
LikeLiked by 1 person
Doesn’t the tight consistency of the fit of the last graph depend on the selection of a Bayesian prior?
LikeLike
Not at all. In this version, there is no fitting of galaxy parameters. We simply plot the data for a constant stellar mass-to-light ratio, which is taken to be the same for all galaxies. WYSISYG. That’s what makes it such a beautiful result.
If you use Bayesian methods to find the best fit galaxy parameters, allowing M*/L to vary within some prior specified by population synthesis models, then the relation becomes tighter still. I wrote about this a few posts back, where you can see the fitted version of the last graph: https://tritonstation.wordpress.com/2018/06/14/rar-fits-to-individual-galaxies/
LikeLike
What I find missing here is any sense of the physical, that is of the physical structure of galactic systems. On just the straightforward observation of a typical galaxy’s structure, supplemented by a rudimentary grasp of the gravitational effect, one would expect to measure some form of gravitational viscosity effect. And that is precisely what your data describes.
It’s long past time to stop coddling the dark matter crowd. Their scandalously lazy, model fixation is nothing to accommodate. It should be identified for what it is, rank scientific incompetence. There is no need to reference a mass discrepancy except as an illustration of the failed analytical model(s) that underlie the claim that such a discrepancy exists.
There simply is no mass discrepancy, that is what your data says, and your data conforms to expectations derived from any reasonable qualitative analysis of galactic structure. That is the case also with regard to galaxy clusters wherein the analysis treats individual galaxies as point sources and ignores the electrodynamic forces that primarily determine the behavior of the plasma that constitutes 90% of the mass of a typical cluster. And the same will doubtless be found true of all the other circumstances where just the right amount of dark matter provides just the necessary corrective to yet another miserable, analytical failure.
Ethan Siegel, in his recent disingenuous piece of claptrap, called you and Sabine Hossenfelder cheats! For science’s sake, man, defend yourself! Wielding the sword of empiricism you can cut clueless mathematicists like that to ribbons. This is no time for collegial timidity. If you are reluctant to defend yourself, at least consider defending the good name of science, which these people have already egregiously tarnished with their empirically baseless, mathematical fantasies.
I do not expect you to publish this. My only hope is that you will consider what is at stake and act accordingly. You have the weapons, now wield them! Of course, if you fear for your career, then you are not the man for the job.
LikeLike
I hadn’t seen the term “mathematicist” before. Seems apropos.
sean s.
LikeLike
Do you have any insight or references for a universe modeled somewhat like a supernova? Specifically where the bang leaves behind a black hole at its center? If space has a positive curvature, then no matter where we pointed our telescopes we would always be looking back toward that center – which may better explain CMB uniformity than the current inflation model. If beyond the CMB lies the mother of all black holes, then cosmic redshift could be viewed as gravitational. Which would lead to a question of how might this universal gravity field affect galaxy rotation?
LikeLike
There has been a dispute since the beginning of the 1980s between two explanations of the discrepancy but… first of all are we sure there is a discrepancy? discrepancy with what? with the expectations at the time of de Vaucouleurs??
https://arxiv.org/abs/1612.07781 : “In summary, the stellar mass model derived from the Gaia star map removes the uncertainties and systematics that could be caused by those on the surface brightness distribution and the constant mass-to-light ratio assumption, and ensure more reliable modelling of the Galaxy. It should be stressed here that with the Galactic disk model proposed in this study, a flat
rotation curve can be generated without using dark matter halos.”
°
I also read that, about the dwarfs: https://arxiv.org/abs/1805.01469
“it implies that dark matter estimate in Milky Way dwarfs cannot be deduced from the product of their radius to the square of their line-of-sight velocity dispersion.”
LikeLike
Do I correctly read these papers to imply that we can forget about DM? or MOND? or both?
I’m not a physicist and I don’t play one on TV…
sean s.
LikeLike
No. We definitely need new physics. These papers only plead the case that we may not need it quite as much as we think in some special cases.
LikeLike
When reading “we definitely need new physics” I immediately think of needing new assumptions. Does the data you show make you question whether the universe is homogeneous on large scales?
LikeLike
What do you mean by new physics, a new mathematical model, a new understanding of the underlying physical processes, or both?
LikeLike
On a very basic level, when really intelligent people conclude that we need new physics or a new model, then why not attack the notion that the universe is homogeneous . . . . and we are at the center of it? I’d say that’s a bit of a stretch.
LikeLike
There are constraints on homogeneity. The early universe is extraordinarily homogeneous, as seen in the cosmic microwave background: one patch of the sky looks very much like the next patch at that time. The universe now is surprisingly far from homogeneity; indeed, this is one of the indicators of new physics: how do we get from the smooth initial condition to where we are today? However, it appears that thing do tend towards homogeneity on very large scales (a few hundred Megaparsecs). While this is much larger than originally expected, it doesn’t do anything to address the basic problems we face.
LikeLike
I wonder if the problem lies in how we got to the conclusion that the early universe was extrextraordinarily homogeneous, when maybe the observations only indicate that it was extraordinarily isotropic?
LikeLike
Just a thought / question…
Are there hard constraints to rule out an additional modification of the gravity at even larger scales (read that as at even lower acceleration scales)? Something like a MOND+.
I’m wondering this as I know MOND cannot explain easily observations at scales larger than galactic ones and still needs to invoke some kind of dark matter (like sterile neutrinos) – i.e. there still is a mass discrepancy.
But isn’t it possible that another modification with a new fundamental acceleration constant (several orders of magnitude lower then a0) past which the strength of the attractive force decays even less than in deep MOND regime could explain the observations?
I mean, you make a very good point in one of your posts that Newton (and Einstein for that matter) formulated the law of attraction based on the observations made at scales in the solar system so it is dangerous to assume directly that the same law must be valid at galactic scales. And here enters MOND which makes very good predictions at these scales…. but then again, is it now safe to assume that MOND must also apply at even larger scales? Why not go further and posit another change at even larger scales?
Of course, MOND is just an empirical law and so this new MOND+ will be, but they would impose strict constraints for a possible underlying theory – i.e. one theory of gravity that in strong fields yields GR, then in normal fields yields Newtonian gravity and in weaker fields MOND and then MOND+(, MOND++ and so on…)
So I repeat, are there hard constraints to exclude such a modification?
LikeLike
The scenario you suggest is quite possible. I prefer not to add +’s to the first modification if it can be helped. But Zhao & Famaey suggested “eMOND” whose Lagrangian has a term that depends on the depth of the potential well as well as acceleration, so can perhaps explain clusters of galaxies.
On a completely speculative note, it occurs to me that while x & t (space & time) are relative, there is an absolute speed (c, the speed of light). So if there is a fundamental dx/dt, why not a fundamental dx/dt^2 (acceleration) and so on for higher order derivatives?
Since the time derivative of an acceleration is a jerk, it would be tempting to identify a Fundamental Jerk with God.
LikeLike
Thank you for the answer.
When you say Zhao and Famaey are you refering to “Unifying all mass discrepancies with one effective gravity law?” (https://arxiv.org/abs/1207.6232)?
Regarding the fundamental acceleration, that’s an interesting thought. However (and using a simplified and not according to the quantum mechanics framework) in this case, how can one propel a photon – i.e. a particle with zero rest mass? Like I said, in a simplified framework – i.e. Newtonian dynamics, you can only exert a force in a limit case if the mass is zero, when the acceleration is infinite. By limiting the maximum acceleration, then there should be another mechanism that allows photon emission becuase zero time something finite is always zero. And no force => no movement => no emitted photon.
LikeLike
Yes, that paper: arxiv:1207.6232. In general, all I meant was that one can imagine other terms appearing in the Lagrangian so that scales besides the acceleration scale matter. Perhaps these are related in some way to a quantization of space-time? This is all speculation… I didn’t suggest a maximum acceleration like a maximum speed, just a special accelerations like Milgrom’s a0. Since c is big and a0 small perhaps the next derivative is a Big Jerk.
LikeLike
Thanks for your anwers…. and nice pun in there, I didn’t expected that.
LikeLike
All we know so far is what doesn’t work. The two well-established pillars of modern physics – General Relativity and the Standard Model of particle physics – do not suffice to describe the universe. They both go along way, and appear to be correct within their respective remit. But there has to be more to the story.
LikeLike
Has there been any research papers that attempt to simulate the universe, and galaxy clusters, with MOND for galaxies, and black holes as dark matter, to explain missing mass MOND doesn’t explain as in galaxy clusters?
could black holes as the dark matter and MOND explain the bullet cluster and large scale structure formation, in combination with MOND?
LikeLike
Yes, in principle black holes could be the lingering dark matter in clusters in MOND. There have been papers that examine this sort of possibility without specifically requiring black holes. It could be pretty much any kind of compact baryonic object (stellar remnants) or neutrinos if they’re massive enough. I’m not particularly fond of any of these ideas, but they are logical possibilities.
LikeLike
The 3rd peak does not necessarily indicate that there is a huge amount of non-baryonic matter, but only that there is a huge amount of collisionless matter, which could be baryonic after all?
LikeLiked by 1 person
The reason General Relativity does not suffice to describe the universe is because the concept of a “universe” is antithetical to GR, invoking as it does a “universal” reference frame. A universal reference frame allows one to speak of a universal “now” and a universal “age” (13.8 Gy). This universal reference frame is inherent to the universal FLRW metric; it is not a consequence of GR. Piggybacking GR on the FLRW metric was and is, a logically inconsistent, analytical error.
Either GR is correct and there is no meaning to the statement, “the universe is 13.8 billion years old” or that is a meaningful statement and GR is falsified. Having it both ways, as is now the approach, is not logically sustainable. Either the concept of singular “universe” has to be jettisoned or GR does. My vote is to retain GR and face the fact that the unitary assumption misrepresents the nature of the cosmos. What is needed, however, is not new physics, just a new conceptual model of the cosmos consistent with GR and observations.
An analogous situation exists on the galactic scale, Neither Newtonian dynamics nor GR necessitate dark matter. The so-called mass discrepancy is simply a consequence of poor analytical modeling. Historically, the Keplerian method has been used to model the expected rotation curves, and it was on the discrepancy of that model’s predicted curves with actual observations, that the dark matter hypothesis was originally proposed. Given the physical inappropriateness of the Keplerian simplification to galactic structures, a mass discrepancy in the results is unavoidable since the Keplerian approach effectively removes all the proximate mass and its gravitational effect from the vicinity of an orbiting body being considered. Models that do not remove mass from the vicinity of the orbiting body such as Feng and Gallo’s and that of the Li paper linked by Nicophil above do not find a mass discrepancy.
Dark matter is a model induced problem as evidenced by your data supporting a RAR. There is no evidence for a mass discrepancy, let alone for dark matter.
LikeLike
Is it too naive to think that the dark matter and dark energy could much more easily be attributed to a black hole at the center of the observable universe? I imagin one could employ the equation Einstein used to successfully predict the anomalies of Mercury’s orbit to find solutions, given the assumption that both the cosmic redshift and galaxy rotation anomalies are due to distant black hole gravity. This seems so much more natural to me. Can anyone give some argument for and against such reasoning?
LikeLike
Well, is there a “center of the observable universe” that is not EARTH? I’d think a black hole located in our solar system with enough mass to explain cosmic events would be … obvious? The observable universe is necessarily centered on us; it’s what’s observable from our POV.
The DM phenomena is not, I think, something that could be explained with a singular mass. The acceleration discrepancy appears to be a galactic phenomena; not a “universal” one (like cosmic expansion is).
does that help at all?
sean s.
LikeLike
I assume that the center of the universe exists beyond as far as we can see, possibly due to an event horizon beyond the CMB. Although it seems like space expands in all directions from an observer, that is not necessarily true if space has positive curvature. Picture that if you look far enough away in any direction, eventually you see back to the same place. We think of an expanding homogeneous space, but that is perhaps the wrong assumption.
LikeLike
Sean,
The galctic data seemed to point to a universal acceleration scale. In trying to wrap my head around that, I think it would make sense if there was an isotropic gravitational field due to a universal black hole looming in the distant background for all observations.
LikeLike
Sean,
In accommodating the existing view that the center of the universe is necessarily centered on the observer, I would call this center the “instantaneous” center. The other center that I described may be thought of as an “eternal” center. This is a bit off topic, but may address the concern that you raised – and does not exclude your POV.
LikeLike
Stacy,
One of the justifications for suggesting that there may be a black hole at the center of the universe is by a simple extension of the Equivalence Principle. This arguably equates the cosmological redshift from relative acceleration to gravitational redshift in an inertial frame.
Not only does it attempt to create a physical model to explain dark energy and dark matter with verified phenomena (things already known to exist), but it provides a strong argument against the Cosmological Principle. This potentially revolutionizes our understanding of the universe. Your work suggests something this proposterous is required.
But is it really that proposterous after all?
LikeLike
There is a supermassive black hole at the center of the Galaxy (4 million solar masses). The universe of galaxies contains many billions of black holes, but it has no physical center. So I am obliged to say yes, what you suggest is really that preposterous.
LikeLike
Stacy,
Much appreciated. Very generally, the notion may only require that space-time is approximately spherical.
Historically humans thought they were at the center of a flat earth, and then later at the center of a celestial shell or sphere. We are pretty good at pattern repetition. Thus at some point we may appreciate the significance of having a physical center to the universe. Do you have a more concrete argument that should be considered?
LikeLike
JB;
Imagining we are at the center of our observable universe is NOT on par with imagining that we are at the center of everything. Since light’s speed is finite and the universe is expanding, there is a distance at which the observable universe ends for any vantage point; including ours. A species located in a far-away galaxy is also at the center of THEIR observable universe. This concept is not human hubris.
Setting aside the question of whether there is any “center” to the universe; I don’t think postulating a massive Cosmic Black Hole (CBH) explains anything.
A CBH does not explain the observed acceleration of cosmic expansion (attributed to “dark energy”) because – so far as I’ve heard – the acceleration is uniform in every direction. If there were a CBH, acceleration would be unbalanced as we were dragged toward the CBH.[*]
And a CBH cannot explain the dynamics of galaxy rotations (attributed to “dark matter” or some “MOND”).
sean s.
[*] you could postulate that the CBH was on the opposite side of a closed universe from us; but that would imply that Earth was in a “special place” in the universe; something I think you’ve already rejected.
LikeLike
Sean,
I think your annotation captures the idea very well. Agreed, the Earth is in a special place. Previously I had mentioned that perhaps the observer is at an “instantaneous” center, but maybe it could also be envisioned as a virtual center.
Presumably the underlying reason why a CBH may effectively describe the observed acceleration is anticipated to be a consequence of the Equivlence Principle.
LikeLike
JB;
I don’t agree that the Earth is in any “special place”; that’s an idea that would demand special evidence. Good luck with that.
“… the observed acceleration is anticipated to be a consequence of the Equivlence Principle.”
I don’t see how that applies.
sean s.
LikeLike
Sean,
I thought you were using the term “Earth” to refer to an observer on Earth. My point is that an observer may be located at the instantaneous or virtual center of the observable universe, which is different than the eternal or physical center. The two being connected by a closed spacetime.
Picture leaving your fellow observer (on Earth let’s say – but it could be anywhere) and travelling in a spaceship in any direction. In the absence of intervening fields you follow a curved geodesic back toward a Cosmic Black Hole. No matter what direction you chose, your fellow observer would begin to see your transmission become progressively redshifted as you moved towards the black hole. But since neither of you knew about the CBH, you might conclude that space was expanding. Perhaps both are valid explanations, but one has virtual dark energy, and the other a CBH.
LikeLike
JB;
I don’t know why, but the site keeps telling me this is a duplicate, but it never actually posts it. I apologize if it does duplicate later.
I think I understand your explanation, but I’m not sure it would work as you suggest. More importantly, your idea requires two things: A CBH (which is a maybe) and the Earth (the planet and all persons on it) to be at a favored position (on the opposite side of the universe from the CBH) which is improbable.
This makes a “dark energy” explanation seem less objectionable; which does not work to your advantage.
Here’s another possibility:
1. There’s no CBH.
2. over time, objects and clusters of objects recede from other objects in the observable universe except for those nearby objects to which they are gravitationally bound.
3. over time, the gravitational influence of very distant objects diminishes as those objects recede.
4. as a consequence, the gravitational “tension” of the observable universe diminishes.
5. since gravitational influence “travels” at the speed of light (or very close to) objects that have receded far enough not only cease to be visible (recession velocity exceeds C), their gravitational influence also goes to zero.
6. over time, as very distant objects recede out of it, the mass of the observable universe decreases; reducing the overall gravitational force within it.
7. the gravitational tension of the observable universe is the only thing that restrains its expansion.
8. so as the observable universe expands, it loses mass, becomes more thinly spread, the resistive force of gravity diminishes, and expansion accelerates.
9. another name for the persistent, expansive force of the universe is “dark energy”.
10. the expansion of the observable universe is accelerating because the expansive force of the universe is more-or-less constant, but the resistive force of gravitational tension is certainly fading.
Probably a crappy theory, but one that really does not need to invoke much that’s new.
sean s.
LikeLike
Sean,
I don’t think that determining how special the Earth and its observers are is a necessary criteria for this theory at this time. That battle can be fought another day. I would just make a hand waving argument that in principle there should be no limit to the number of instantaneous or virtual centers in the spacetime.
What is important is that in principle the mass and distance to the Cosmic Black Hole could be calculated, and maybe incorporated in models of the early universe.
LikeLike
What do you think of this paper on SIDM dark matter reproducing the RAR? https://arxiv.org/pdf/1808.05695.pdf
LikeLike
An SIDM model has several interesting implications. It makes it more likely that DM consists of multiple types of particles or fields, and yet we can find none of them so far.
Given how our experiments are usually conducted (“high-energy” particle interactions) this would indicate that the particles we are familiar with (non-dark matter) do not interact with any DM particles/fields at all. Except for gravity.
I remember several years ago a proposal on why—perhaps—gravity is so weak as compared to the other forces. The idea was that there were many dimensions (10+) and the particles we are familiar with are all constrained to act just within our 3 familiar dimensions (ignoring time). However, perhaps gravity acts across all 10+ dimensions, and is thus diluted.
If there is a “dark sector” mirroring our familiar sector; is in possible that the particles and fields there are similarly constrained and the only way our matter interacts with dark matter is gravitationally?
Would this mean the Higgs field (?) has to span all dimensions too?
Could the “dark sector” be a “parallel universe”?
sean s.
LikeLike
SIDM is beyond the scope of this discussion. The claims about how well it works seem overblown to me.
LikeLike
I accept your judgement; it’s way outside my wheelhouse.
sean s.
LikeLike
When I look at the figures I see a very convincing relationship that needs to be explained, and it really seems unlikely it will be some sort of “dark matter” in the sense that term is usually used.
However, I also don’t see any discontinuity at ~10^-10 m/s^2. I see a gradual/continuous deviation that obviously follows some sort of mathematical law.
The “obsession” with this number is something that confuses me about MOND. Isn’t it just an arbitrary point where “statistical significance” of some kind or the other is being decided?
Apologies if that is a dumb or well known question.
LikeLike
Yes, the transition is gradual. It was stipulated to be smooth, at a particular acceleration scale. It could have been more abrupt, but the point is that there is this change. So one has to mark it somehow. The exact value of the acceleration scale depends on how you define the transition. There are a number of distinct approaches that I described in a recent conference presentation
Click to access AScale_cosmicsignatures.pdf
They all consistently come up with the same number, to astronomical accuracy. By necessity, it is a point along the transition, not a sharp discontinuity.
LikeLike