I have been wanting to write about dwarf satellites for a while, but there is so much to tell that I didn’t think it would fit in one post. I was correct. Indeed, it was worse than I thought, because my own experience with low surface brightness (LSB) galaxies in the field is a necessary part of the context for my perspective on the dwarf satellites of the Local Group. These are very different beasts – satellites are pressure supported, gas poor objects in orbit around giant hosts, while field LSB galaxies are rotating, gas rich galaxies that are among the most isolated known. However, so far as their dynamics are concerned, they are linked by their low surface density.
Where we left off with the dwarf satellites, circa 2000, Ursa Minor and Draco remained problematic for MOND, but the formal significance of these problems was not great. Fornax, which had seemed more problematic, was actually a predictive success: MOND returned a low mass-to-light ratio for Fornax because it was full of young stars. The other known satellites, Carina, Leo I, Leo II, Sculptor, and Sextans, were all consistent with MOND.
The Sloan Digital Sky Survey resulted in an explosion in the number of satellites galaxies discovered around the Milky Way. These were both fainter and lower surface brightness than the classical dwarfs named above. Indeed, they were often invisible as objects in their own right, being recognized instead as groupings of individual stars that shared the same position in space and – critically – velocity. They weren’t just in the same place, they were orbiting the Milky Way together. To give short shrift to a long story, these came to be known as ultrafaint dwarfs.
Ultrafaint dwarf satellites have fewer than 100,000 stars. That’s tiny for a stellar system. Sometimes they had only a few hundred. Most of those stars are too faint to see directly. Their existence is inferred from a handful of red giants that are actually observed. Where there are a few red giants orbiting together, there must be a source population of fainter stars. This is a good argument, and it is likely true in most cases. But the statistics we usually rely on become dodgy for such small numbers of stars: some of the ultrafaints that have been reported in the literature are probably false positives. I have no strong opinion on how many that might be, but I’d be really surprised if it were zero.
Nevertheless, assuming the ultrafaints dwarfs are self-bound galaxies, we can ask the same questions as before. I was encouraged to do this by Joe Wolf, a clever grad student at UC Irvine. He had a new mass estimator for pressure supported dwarfs that we decided to apply to this problem. We used the Baryonic Tully-Fisher Relation (BTFR) as a reference, and looked at it every which-way. Most of the text is about conventional effects in the dark matter picture, and I encourage everyone to read the full paper. Here I’m gonna skip to the part about MOND, because that part seems to have been overlooked in more recent commentary on the subject.
For starters, we found that the classical dwarfs fall along the extrapolation of the BTFR, but the ultrafaint dwarfs deviate from it.

The deviation is not subtle, at least not in terms of mass. The ultrataints had characteristic circular velocities typical of systems 100 times their mass! But the BTFR is steep. In terms of velocity, the deviation is the difference between the 8 km/s typically observed, and the ~3 km/s needed to put them on the line. There are a large number of systematic effects errors that might arise, and all act to inflate the characteristic velocity. See the discussion in the paper if you’re curious about such effects; for our purposes here we will assume that the data cannot simply be dismissed as the result of systematic errors, though one should bear in mind that they probably play a role at some level.
Taken at face value, the ultrafaint dwarfs are a huge problem for MOND. An isolated system should fall exactly on the BTFR. These are not isolated systems, being very close to the Milky Way, so the external field effect (EFE) can cause deviations from the BTFR. However, these are predicted to make the characteristic internal velocities lower than the isolated case. This may in fact be relevant for the red points that deviate a bit in the plot above, but we’ll return to that at some future point. The ultrafaints all deviate to velocities that are too high, the opposite of what the EFE predicts.
The ultrafaints falsify MOND! When I saw this, all my original confirmation bias came flooding back. I had pursued this stupid theory to ever lower surface brightness and luminosity. Finally, I had found where it broke. I felt like Darth Vader in the original Star Wars:

The first draft of my paper with Joe included a resounding renunciation of MOND. No way could it escape this!
But…
I had this nagging feeling I was missing something. Darth should have looked over his shoulder. Should I?
Surely I had missed nothing. Many people are unaware of the EFE, just as we had been unaware that Fornax contained young stars. But not me! I knew all that. Surely this was it.
Nevertheless, the nagging feeling persisted. One part of it was sociological: if I said MOND was dead, it would be well and truly buried. But did it deserve to be? The scientific part of the nagging feeling was that maybe there had been some paper that addressed this, maybe a decade before… perhaps I’d better double check.
Indeed, Brada & Milgrom (2000) had run numerical simulations of dwarf satellites orbiting around giant hosts. MOND is a nonlinear dynamical theory; not everything can be approximated analytically. When a dwarf satellite is close to its giant host, the external acceleration of the dwarf falling towards its host can exceed the internal acceleration of the stars in the dwarf orbiting each other – hence the EFE. But the EFE is not a static thing; it varies as the dwarf orbits about, becoming stronger on closer approach. At some point, this variation becomes to fast for the dwarf to remain in equilibrium. This is important, because the assumption of dynamical equilibrium underpins all these arguments. Without it, it is hard to know what to expect short of numerically simulating each individual dwarf. There is no reason to expect them to remain on the equilibrium BTFR.
Brada & Milgrom suggested a measure to gauge the extent to which a dwarf might be out of equilibrium. It boils down to a matter of timescales. If the stars inside the dwarf have time to adjust to the changing external field, a quasi-static EFE approximation might suffice. So the figure of merit becomes the ratio of internal orbits per external orbit. If the stars inside a dwarf are swarming around many times for every time it completes an orbit around the host, then they have time to adjust. If the orbit of the dwarf around the host is as quick as the internal motions of the stars within the dwarf, not so much. At some point, a satellite becomes a collection of associated stars orbiting the host rather than a self-bound object in its own right.
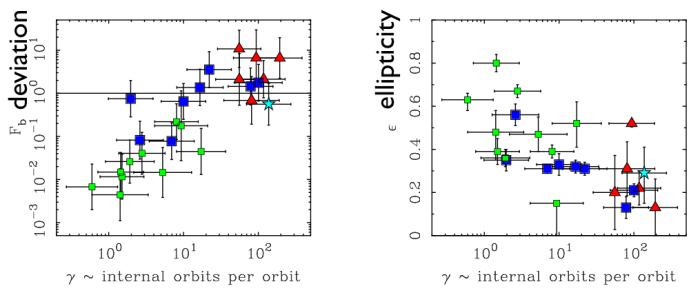
Brada & Milgrom provide the formula to compute the ratio of orbits, shown in the figure above. The smaller the ratio, the less chance an object has to adjust, and the more subject it is to departures from equilibrium. Remarkably, the amplitude of deviation from the BTFR – the problem I could not understand initially – correlates with the ratio of orbits. The more susceptible a dwarf is to disequilibrium effects, the farther it deviated from the BTFR.
This completely inverted the MOND interpretation. Instead of falsifying MOND, the data now appeared to corroborate the non-equilibrium prediction of Brada & Milgrom. The stronger the external influence, the more a dwarf deviated from the equilibrium expectation. In conventional terms, it appeared that the ultrafaints were subject to tidal stirring: their internal velocities were being pumped up by external influences. Indeed, the originally problematic cases, Draco and Ursa Minor, fall among the ultrafaint dwarfs in these terms. They can’t be in equilibrium in MOND.
If the ultrafaints are out of equilibrium, the might show some independent evidence of this. Stars should leak out, distorting the shape of the dwarf and forming tidal streams. Can we see this?
A definite maybe:

The dwarfs that are more subject to external influence tend to be more elliptical in shape. A pressure supported system in equilibrium need not be perfectly round, but one departing from equilibrium will tend to get stretched out. And indeed, many of the ultrafaints look Messed Up.
I am not convinced that all this requires MOND. But it certainly doesn’t falsify it. Tidal disruption can happen in the dark matter context, but it happens differently. The stars are buried deep inside protective cocoons of dark matter, and do not feel tidal effects much until most of the dark matter is stripped away. There is no reason to expect the MOND measure of external influence to apply (indeed, it should not), much less that it would correlate with indications of tidal disruption as seen above.
This seems to have been missed by more recent papers on the subject. Indeed, Fattahi et al. (2018) have reconstructed very much the chain of thought I describe above. The last sentence of their abstract states “In many cases, the resulting velocity dispersions are inconsistent with the predictions from Modified Newtonian Dynamics, a result that poses a possibly insurmountable challenge to that scenario.” This is exactly what I thought. (I have you now.) I was wrong.
Fattahi et al. are wrong for the same reasons I was wrong. They are applying equilibrium reasoning to a non-equilibrium situation. Ironically, the main point of the their paper is that many systems can’t be explained with dark matter, unless they are tidally stripped – i.e., the result of a non-equilibrium process. Oh, come on. If you invoke it in one dynamical theory, you might want to consider it in the other.
To quote the last sentence of our abstract from 2010, “We identify a test to distinguish between the ΛCDM and MOND based on the orbits of the dwarf satellites of the Milky Way and how stars are lost from them.” In ΛCDM, the sub-halos that contain dwarf satellites are expected to be on very eccentric orbits, with all the damage from tidal interactions with the host accruing during pericenter passage. In MOND, substantial damage may accrue along lower eccentricity orbits, leading to the expectation of more continuous disruption.
Gaia is measuring proper motions for stars all over the sky. Some of these stars are in the dwarf satellites. This has made it possible to estimate orbits for the dwarfs, e.g., work by Amina Helmi (et al!) and Josh Simon. So far, the results are definitely mixed. There are more dwarfs on low eccentricity orbits than I had expected in ΛCDM, but there are still plenty that are on high eccentricity orbits, especially among the ultrafaints. Which dwarfs have been tidally affected by interactions with their hosts is far from clear.
In short, reality is messy. It is going to take a long time to sort these matters out. These are early days.
Great writing. There is a real sense of suspense when you say that we are just in the early days of our understanding of said discrepencies – the kind where you wonder “what does he really mean?”
Anyway, I have a question that is in the context of the relatively recent confidence that the universe is flat. Is the common representation of an alternative, for example a positively curved universe, being considered carefully enough? Specifically, there is often depicted a sphere with an arbitrary triangle drawn thereupon to indicate that the sum of the internal angles is >180 deg. I understand also that it is inferred that many observations do not fit with the notion of such curvature.
My question is, why must we consider this arbitrary triangle as analogous to having some physical representation in the space-time? In the case of the surface of a sphere, could the “triangle” be transformed upon a great circle such that the object is at one pole and the observer is at the other? If for example, an observer were to look at perhaps the most distant object in the universe, say the CMB, then can we rightly expect the observer and object to be at opposite poles of what could be a positively curved universe, and then how would we know the curvature in that case?
LikeLike
The empirical constrain is that the geometry of the universe has to be very close to flat in the context of the Robertson-Walker metric. Of course, it is one of the goals of observational cosmology to test whether that is the correct metric. It appears adequate so far, provided we have dark matter and dark energy in exactly the right amounts.
As for triangles, perhaps another way to think of it is the propagation of parallel light beams. Set up two lasers to fire a beam that is perfectly parallel, then come back and check on them after they’ve traversed a Gigaparsec or a few. If the geometry is flat, they will remain exactly parallel. If the geometry is closed, the beams will converge, like lines of constant longitude on a globe as you approach the pole. The pole may be a convenient fiction, but we can’t transform our way out of the convergence – that’s the point of the triangles-on-a-sphere analogy.
LikeLike
You make a good point about evaluating the metric empirically. I wanted to suggest we may not be considering enough possibilities to infer that the universe must be flat, but as you say, the correct inference is that the universe in the context of the FR metric is likely flat.
More generally, I wonder if it is being considered enough to embed a duality at the cosmological horizon, which is perhaps analogous to the duality in quantum mechanics. Specifically, we may have a dynamic and flat universe that is nearly infinite in size and finite in age, which is complementary to a static and curved universe that is finite in size and infinite in age. If this is a worthwhile pursuit, though it may be a great challenge, there would be little point in arguing about which is the right universe. What do you think about such a suggestion?
LikeLike
> the result of a non-equilibrium process. Oh, come on. If you invoke it in one dynamical theory, you might want to consider it in the other.
My rank amateur intuition is that finding a system that *is* out of equilibrium is surprising, but finding a system that *was* out of equilibrium is par for the course. What am I misunderstanding here? Is it simply that the probability of a system being tidally stripped of dark matter is much, much lower than the probability of a dwarf being out of equilibrium?
LikeLike
You are exactly right – disequilibrium situations should be rare, brutish, and short. What we mean by short differs between the theories, and what we can observe is different. Tidal stripping is an ever-occurring process in CDM, but is only noticeable in the aftermath – the dark matter is affected continuously, but we can only notice it when so much DM is stripped away that the stars become affected. The timescale is longer in MOND but there is no protective cocoon of DM, so we could in principle notice the stars being stripped as soon as it starts to happen. In either case, it is actually rather hard to tell in practice.
There are real differences though. The messed up systems pictured above have high conventional M/L – they should no yet be subject to visible tidal effects in DM. And yet. On the other hand, you are correct that a system has time to settle after being stripped in CDM, so we ought to see those in a probabilistic sense.
What trouble me is that there is, at present, no criterion for when this has or has not happened in CDM. We basically throw our hands up and say any dwarf that doesn’t make sense must have been worked over by the local thugs at some point in the past. Maybe so, but there is no way at present to say *this* dwarf was tidally disrupted; *that* one was not. In contrast, there is a criterion In MOND. The messed-up galaxies meet this criterion. Those that aren’t, don’t: And XXVIII is an example – a problem there could not be excused in this fashion.
It is my hope that LSST or other projects will discover lots of new, very low mass galaxies far removed from the possibility of these types of influences. Then neither theory can hide behind these skirts. In LCDM, an ultrafaint dwarf in the field must look like it lives in a pristine NFW halo. In MOND, it has to fall on the BTFR. For a dwarf like Crater 2, that’s a difference between a velocity dispersion of 17 and 4 km/s, respectively.
LikeLiked by 2 people
Many years ago, before I was even (for a short time) a professional astronomer, I used to analyse perturbations of cometary orbits for the BAA. What you are describing reminded me of the way that meteor showers are associated with comets and spread along their orbits. So, I was wondering if you started with a Galactic potential and modelled test particles moving within it (including a suitable level of self-attraction between the test particles) whether you could demonstrate a link between ellipticity and the internal orbits/orbit ratio.
LikeLike
Great question. Given ample time and resources, I would certainly like to investigate it. I have made some small starts, but it is a bigger problem than I have been able to address myself in my copious spare time.
To some extent, Brada & Milgrom have already done this. But they were talking in generic terms. Now that stuff is getting real, one needs object-specific simulations.
LikeLike
Is the Sparc data relevant to this topic? If so, have you been able to analyse it for comparison with your 2010 data?
LikeLike
The data for rotating galaxies (the gray points in the first figure) is a precursor to SPARC. So there are more data now, and the extend a bit lower in mass… the dwarf Irregular Leo P (not part of SPARC) is basically indistinguishable from Fornax on the BTFR. But nothing else [yet] probes the ultrafaint regime: these objects are only know because of their extreme proximity to the Milky Way. They are literally in our cosmic backyard. Hence my hope that we’ll be able to discover more farther away… the trick there will be obtaining accurate spectroscopic measurements of their internal velocities. But we gotta discover them first.
LikeLike
Great blogpost. I learned so much. Thanks.
EFE for parallel and orthogonal external fields. I do understand the conceptual origin of the EFE in Mondian mechanics : internal and external fields are vectorally added and the magnitude of the result inserted into the interpolation function. Rather surprisingly this scheme predicts a pure ‘ transverse EFE’ : the internal dynamics is effected by a field orthogonal to the internal field. Very Machian!!! My question : is there direct observational evidence for a ‘ transverse EFE’?
I noticed that in numerical calculations the field vectors are somehow projected on 1D and then the magnitudes added ( for example in your paper discussing NGC1052-DF2).I guess this is completely adequate for the case at hand.
To distinguish between transverse and parallel EFE for nearby systems, MW or MG31, we needed a rotationally supported satellite in equlibrium ( I guess). Are there any?
LikeLike
Curious! Do you have references on this I could look into or some other info?
LikeLike
There is good evidence among the dwarfs that the EFE is active, which is itself an important test. I have looked for a directional effect in the satellites of Andromeda, but such a signal is subtle, if present, and current data aren’t up to spotting it.
LikeLike
mind. blown.
LikeLike
The consequences would certainly seem to be very far reaching. Woud it be possible to send you a very short draft that outlines the theory a litte better for your review? If so, could you send me an email at jamesbraun@siemens.com?
LikeLike
It’s been a while but I’d be interested to read anything you have on that! My mail address is markhuisjes@hotmail.com
LikeLike
This paper may be on point. Hai Yu, Bharat Ratra, Fa-Yin Wang, “Dark matter deficient galaxies in the Illustris flat-ΛCDM model structure formation simulation” (September 16, 2018). https://arxiv.org/abs/1809.05938 It continues the discussion of NGC1052-DF2.
LikeLike
While I’m strongly in favor of a MOND approach to solving the anomalously high rotation rates in the galactic suburbs, from my layman’s perspective I’ve long been bothered by the seemingly implied violation of energy conservation. If the ‘stuff’ in the outer reaches of galaxies is moving faster than allowed by Newton and General Relativity, then the galaxy as a system is exhibiting more energy than is permitted by standard physics.
Another question is whether our solar system is far enough out from the Milky Way’s center for Mordehai Milgrom’s acceleration scale (a0) to kick in.
LikeLike
To answer the second question first, the Milky Way is pretty high surface brightness, so close to the Newtonian regime. Where we live, the centripetal acceleration is about 1.8 a0. So we are not far enough out for MOND effects to kick in strongly; we are in the transition region.
Energy conservation is a deeper question. Your intuition is correct; Milgrom’s first (1983) proposal did not conserve energy – a serious problem! This was rectified with the so-called aquadratic lagrangian proposed by Bekenstein & Milgrom in 1984, in which they derived a modified Poisson equation that does conserve energy. This is more straightforward than it might sound.
LikeLike
Thank you, Stacy, for the responses. I’ll have to look up that paper by Bekenstein & Milgrom to try to understand the detailed mechanism by which energy can be conserved in the MONDian approach.
LikeLike
Stacy – on the streams – have you looked at this talk at the Perimeter by Ana Bonaca? To me, it seems unlikely that dark matter exists in the super compact ‘points’ as their data suggests. It’s a good talk. https://www.perimeterinstitute.ca/videos/uncovering-nature-dark-matter-stellar-streams-milky-way
LikeLike
I have not seen this particular talk.
Certainly the smoothness or lumpiness of streams contains information about the continuity or granularity of the underlying gravitational potential. In practice, it may take a while to sort out – I have heard contradictory assertions. I suspect part of the challenge is that real-world streams are not guaranteed to be a simple as an idealized continuum of stars where any gap can be interpreted as being caused by a lump of dark matter. In time, it should be possible to sort out with enough examples.
LikeLike
A recent paper located here (https://doi.org/10.1364/OPTICA.5.000942) claims to have derived an identity between measures of entanglement and duality. If the suggestion that the loss of entanglement increases duality and vice versa, how important might this observation be in resolving questions about dark matter and dark energy?
LikeLike
Off hand, there is no obviously relevant connection. It is conceivable that there is something to the quantum nature of space-time that might entangle the tiny with our cosmic conundrums, but that would be pure speculation.
LikeLike
Yes, and it is not lost on me how taxing it must be to respond to speculation, when the focus is really on getting to more solid ground – so thank you for thoughtfully keeping such discussions open.
With regard to this particular discussion about whether entanglement/duality relationships are meaningful in cosmology: emerging from our cosmic conundrums without redefining our horizons would be rather uncharacteristic of us. So how we define our horizons is probably critical, but it also seems very fuzzy at the moment (one proposed solution to the black hole firewall paradox is the “fuzzball”).
I think we need to straighten out some of these paradoxes at our horizons before the cosmological picture really clears up.
LikeLike
The recent discovery of a dwarf spheroidal galaxy in the direction of the globular cluster NGC6752, reported in https://academic.oup.com/mnrasl/article/484/1/L54/5288002 might offer an opportunity to test MOND if it is sufficently far from the spiral NGC 6744 to be outside the EFE.
LikeLike
Sure. I look forward to more such discoveries, especially of tiny dwarfs in the voids, far from any external influences. Of course, we already have had many such opportunities, and one wants to test MOND both with and without the EFE. E.g., And XXVIII was a dwarf of Andromeda that we pointed out was one of the best tests of an isolated system; two independent measurements corroborated the MOND predicted velocity dispersion. In the opposite regime, both And XIX and Crater 2 are extreme objects that were both entirely unanticipated conventionally but accurately predicted with the EFE in MOND. Which is all to say, yes, of course we should keep testing it – but we’ve already done that for literally hundreds of galaxies, so at some point enough is enough. I think the more interesting things for isolated void dwarfs is that, if tiny enough, the should behave like pristine NFFW halos. How tiny and how isolated they need to be is a moving target.
LikeLike