The missing mass problem has been with us many decades now. Going on a century if you start counting from the work of Oort and Zwicky in the 1930s. Not quite a half a century if we date it from the 1970s when most of the relevant scientific community started to take it seriously. Either way, that’s a very long time for a major problem to go unsolved in physics. The quantum revolution that overturned our classical view of physics was lightning fast in comparison – see the discussion of Bohr’s theory in the foundation of quantum mechanics in David Merritt’s new book.
To this day, despite tremendous efforts, we have yet to obtain a confirmed laboratory detection of a viable dark matter particle – or even a hint of persuasive evidence for the physics beyond the Standard Model of Particle Physics (e.g., supersymmetry) that would be required to enable the existence of such particles. We cannot credibly claim (as many of my colleagues insist they can) to know that such invisible mass exists. All we really know is that there is a discrepancy between what we see and what we get: the universe and the galaxies within it cannot be explained by General Relativity and the known stable of Standard Model particles.
If we assume that General Relativity is both correct and sufficient to explain the universe, which seems like a very excellent assumption, then we are indeed obliged to invoke non-baryonic dark matter. The amount of astronomical evidence that points in this direction is overwhelming. That is how we got to where we are today: once we make the obvious, imminently well-motivated assumption, then we are forced along a path in which we become convinced of the reality of the dark matter, not merely as a hypothetical convenience to cosmological calculations, but as an essential part of physical reality.
I think that the assumption that General Relativity is correct is indeed an excellent one. It has repeatedly passed many experimental and observational tests too numerous to elaborate here. However, I have come to doubt the assumption that it suffices to explain the universe. The only data that test it on scales where the missing mass problem arises is the data from which we infer the existence of dark matter. Which we do by assuming that General Relativity holds. The opportunity for circular reasoning is apparent – and frequently indulged.
It should not come as a shock that General Relativity might not be completely sufficient as a theory in all circumstances. This is exactly the motivation for and the working presumption of quantum theories of gravity. That nothing to do with cosmology will be affected along the road to quantum gravity is just another assumption.
I expect that some of my colleagues will struggle to wrap their heads around what I just wrote. I sure did. It was the hardest thing I ever did in science to accept that I might be wrong to be so sure it had to be dark matter – because I was sure it was. As sure of it as any of the folks who remain sure of it now. So imagine my shock when we obtained data that made no sense in terms of dark matter, but had been predicted in advance by a completely different theory, MOND.
When comparing dark matter and MOND, one must weigh all evidence in the balance. Much of the evidence is gratuitously ambiguous, so the conclusion to which one comes depends on how one weighs the more definitive lines of evidence. Some of this points very clearly to MOND, while other evidence prefers non-baryonic dark matter. One of the most important lines of evidence in favor of dark matter is the acoustic power spectrum of the cosmic microwave background (CMB) – the pattern of minute temperature fluctuations in the relic radiation field imprinted on the sky a few hundred thousand years after the Big Bang.
The equations that govern the acoustic power spectrum require General Relativity, but thankfully the small amplitude of the temperature variations permits them to be solved in the limit of linear perturbation theory. So posed, they can be written as a damped and driven oscillator. The power spectrum favors features corresponding to standing waves at the epoch of recombination when the universe transitioned rather abruptly from an opaque plasma to a transparent neutral gas. The edge of a cloud provides an analog: light inside the cloud scatters off the water molecules and doesn’t get very far: the cloud is opaque. Any light that makes it to the edge of the cloud meets no further resistance, and is free to travel to our eyes – which is how we perceive the edge of the cloud. The CMB is the expansion-redshifted edge of the plasma cloud of the early universe.
An easy way to think about a damped and a driven oscillator is a kid being pushed on a swing. The parent pushing the child is a driver of the oscillation. Any resistance – like the child dragging his feet – damps the oscillation. Normal matter (baryons) damps the oscillations – it acts as a net drag force on the photon fluid whose oscillations we observe. If there is nothing going on but General Relativity plus normal baryons, we should see a purely damped pattern of oscillations in which each peak is smaller than the one before it, as seen in the solid line here:
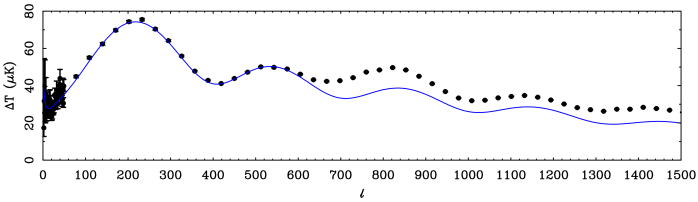
As one can see, the case of no Cold Dark Matter (CDM) does well to explain the amplitudes of the first two peaks. Indeed, it was the only hypothesis to successfully predict this aspect of the data in advance of its observation. The small amplitude of the second peak came as a great surprise from the perspective of LCDM. However, without CDM, there is only baryonic damping. Each peak should have a progressively lower amplitude. This is not observed. Instead, the third peak is almost the same amplitude as the second, and clearly higher than expected in the pure damping scenario of no-CDM.
CDM provides a net driving force in the oscillation equations. It acts like the parent pushing the kid. Even though the kid drags his feet, the parent keeps pushing, and the amplitude of the oscillation is maintained. For the third peak at any rate. The baryons are an intransigent child and keep dragging their feet; eventually they win and the power spectrum damps away on progressively finer angular scales (large 𝓁 in the plot).
As I wrote in this review, the excess amplitude of the third peak over the no-CDM prediction is the best evidence to my mind in favor of the existence of non-baryonic CDM. Indeed, this observation is routinely cited by many cosmologists to absolutely require dark matter. It is argued that the observed power spectrum is impossible without it. The corollary is that any problem the dark matter picture encounters is a mere puzzle. It cannot be an anomaly because the CMB tells us that CDM has to exist.
Impossible is a high standard. I hope the reader can see the flaw in this line of reasoning. It is the same as above. In order to compute the oscillation power spectrum, we have assumed General Relativity. While not replacing it, the persistent predictive successes of a theory like MOND implies the existence of a more general theory. We do not know that such a theory cannot explain the CMB until we develop said theory and work out its predictions.
That said, it is a tall order. One needs a theory that provides a significant driving term without a large amount of excess invisible mass. Something has to push the swing in a universe full of stuff that only drags its feet. That does seem nigh on impossible. Or so I thought until I heard a talk by Pedro Ferreira where he showed how the scalar field in TeVeS – the relativistic MONDian theory proposed by Bekenstein – might play the same role as CDM. However, he and his collaborators soon showed that the desired effect was indeed impossible, at least in TeVeS: one could not simultaneously fit the third peak and the data preceding the first. This was nevertheless an important theoretical development, as it showed how it was possible, at least in principle, to affect the peak ratios without massive amounts of non-baryonic CDM.
At this juncture, there are two options. One is to seek a theory that might work, and develop it to the point where it can be tested. This is a lot of hard work that is bound to lead one down many blind alleys without promise of ultimate success. The much easier option is to assume that it cannot be done. This is the option adopted by most cosmologists, who have spent the last 15 years arguing that the CMB power spectrum requires the existence of CDM. Some even seem to consider it to be a detection thereof, in which case we might wonder why we bother with all those expensive underground experiments to detect the stuff.
Rather fewer people have invested in the approach that requires hard work. There are a few brave souls who have tried it; these include Constantinos Skordis and Tom Złosnik. Very recently, the have shown a version of a relativistic MOND theory (which they call RelMOND) that does fit the CMB power spectrum. Here is the plot from their paper:

Note that black line in their plot is the fit of the LCDM model to the Planck power spectrum data. Their theory does the same thing, so it necessarily fits the data as well. Indeed, a good fit appears to follow for a range of parameters. This is important, because it implies that little or no fine-tuning is needed: this is just what happens. That is arguably better than the case for LCDM, in which the fit is very fine-tuned. Indeed, that was a large point of making the measurement, as it requires a very specific set of parameters in order to work. It also leads to tensions with independent measurements of the Hubble constant, the baryon density, and the amplitude of the matter power spectrum at low redshift.
As with any good science result, this one raises a host of questions. It will take time to explore these. But this in itself is a momentous result. Irrespective if RelMOND is the right theory or, like TeVeS, just a step on a longer path, it shows that the impossible is in fact possible. The argument that I have heard repeated by cosmologists ad nauseam like a rosary prayer, that dark matter is the only conceivable way to explain the CMB power spectrum, is simply WRONG.
Does RelMOND have a physical basis? How do they arrive at the RelMOND formulas?
LikeLike
1. I remain mystified as to WHY MOND happens. It is a fundamental question.
2. You’ll have to read their paper to follow the derivation.
LikeLiked by 2 people
MOND follows from quantum inertia, using the neutrino CMB correspondence for the non local vacuum. Done deal.
LikeLike
My admittedly unusual research is based on immutable charged Planck spheres in a 3D Euclidean void. The first structure that emerges is a Riemannian spacetime made of charged Planck spheres in various configurations. All other matter-energy particles emerge as well. I think of spacetime as possibly being composed of different fundamental ‘gases’ for lack of a better term. So, when I look at the power spectrum picture, it looks to me like the sum of the black body curves for six different particles that tend to comprise the spacetime aether.
Again, thank you Stacy for allowing me to comment.
LikeLike
Just brainstorming here. But if the CMB power spectrum is the sum of the black body radiation of multiple composite Planck sphere particles, then that first big peak could be the lowest energy particle that is somewhat stable. Maybe a very tired photon. Or maybe some product of a reaction of very tired photons and neutrinos? Then maybe the next several humps are additioinal emergence, The reaction product of when particles from the first peak are involved? If this were all correct, then it might follow that these random reactions of low energy spacetime aether particles must be guaranteed to produce some standard matter particles of enough energy that they begin convecting through the aether towards higher matter-energy density. And this is a portion of the galaxy local recycling process.
LikeLike
Brilliant!
I’ll gave to sit some time with this.
But just out of curiosity – if this is going to be a big next step, would Milgrom get a Nobel? Or just the authors of this paper?
LikeLike
Milgrom deserves a Nobel prize simply for identifying the importance of the acceleration scale. This is effectively a new constant of nature akin to Planck’s constant. Many others deserve a prize as well – Bob Sanders, Bekenstein (unfortunately deceased)… this topic is more important that a single prize. Certainly more important than the series of prizes that were handed out for discovering new particles in the ’60s.
LikeLiked by 1 person
That means that he should receive a Nobel even if this doesn’t pan out?
Do you think this would be possible given the current situation in cosmology?
LikeLike
1. Yes. 2. No.
What, exactly, has to pan out? And what is it that we award Nobel prizes for?
See https://tritonstation.com/2016/07/18/natural-law/
LikeLiked by 1 person
Thanks Stacy, very interesting post and paper
About “the universe and the galaxies within it cannot be explained by General Relativity and the known stable of Standard Model particles”, and specifically the GR part:
It seems to me that we currently do not have a full understanding of even classical (that is, not quantum) GR effects in cosmology. I’m referring mostly to the question of whether the late universe can really be described by FLRW (that is, the backreaction program, that seems alive as far as I can tell). While this is most often discussed in the context of dark energy, there are some suggestions for relations to dark matter. Don’t you think there could be some progress coming just from understanding classical GR effects better?
LikeLike
Not much. We do cling to homogeneity and isotropy for the background FLRW solution, and I do worry that these might not hold in the late universe. So yes, we do need to worry about things like backreaction. But there is practically zero chance that GR by itself is going to dig us out of these problems.
LikeLike
Stacy,
if dark matter particles in the form of sterile neutrinos, axions, neutralinos, or even “fifth force” X17 boson is confirmed, what does this imply for MOND? could MOND and dark matter both be correct?
LikeLike
The answer depends on each case. For each case, it further depends on the mass and number of particles. Axions could exist for the particle physics reasons they were originally imagined and yet have nothing to do with the dark matter problem. Sterile neutrinos could be the dark matter if the exist in the right mass (the keV range in some models) and sufficient numbers. They have also been considered in the context of MOND (in the 11 eV range) as a solution to the cluster missing mass problem and the third peak of the CMB. Neutralinos are the presumptive favorite flavor of WIMPs, which if they exist with the right mass and density would effectively confirm the traditional CDM picture. So… it depends.
In principle, both MOND and DM could be correct, but that would suck. Invoking both buggers Occam’s razor (which is the primary reason I become interested in MOND: it provides a much tidier explanation of mass discrepancies that DM) and smacks of the hybrid model of Tycho Brahe: trying to have the best of both worlds is really the worst of both. If something like WIMP DM exists, it would be impossible to prevent it from sticking to galaxies, in which case MOND would act on both DM and stars, so that wouldn’t work. One can come up with MOND-compliant variants of dark matter (like Khoury’s superfluid DM) but that’s not really having both, it is having DM that results in MOND-like behavior.
In short, I will be very disappointed in the Universe if it does both MOND and dark matter.
LikeLiked by 2 people
thanks for this answer,
re “They have also been considered in the context of MOND (in the 11 eV range) as a solution to the cluster missing mass problem”
if you want a MOND only explanation, what do you think is the solution for cluster missing mass problem? could a new type of MOND by changing gravity yet again for clusters solve it? or perhaps MOND and acceleration is incorrect and gravity has to be modified in some way that explains both individual galaxy rotations curves AND galaxy clusters?
LikeLike
I don’t know what the solution for the cluster missing mass problem is – in either theory. I discuss this in part at https://tritonstation.com/2016/08/06/missing-baryons-in-lcdm-and-mond/ Another possibility, as you say, is that MOND is just an approximation, and there is something more to is in clusters; as example of such an idea is discussed in https://arxiv.org/abs/1207.6232
LikeLiked by 1 person
Hello,
I have read the article but I do not have academic knowledge in cosmology. From what I understand, relMOND needs a scalar field and vector field but what is their physical meaning ? If you add a scalar field, does it imply a corresponding particle ?
LikeLiked by 1 person
Good questions.
LikeLike
@Alexandre, in the Skordis and Zlosnik paper arXiv:2007.00082, only the metric and the vector field are “fundamental”, i.e., actual “dynamical variables”. The scalars are “nondynamical” auxiliary variables that are introduced only to simplify the math, and can ultimately be reexpressed as functions of the metric and vector fields — which BTW is also true of the nondynamical “second metric” and nondynamical “scalar field” in TeVeS, as previously shown by Zlosnik, Ferreira, and Starkman in arXiv:gr-qc/0606039.
In reality, TeVeS is likewise just an instance of a “Tensor-Vector” gravity theory, with no “scalar” — albeit it is somewhat “exotic” compared to most previously-studied Tensor-Vector theories because the vector field has a nonstandard “Kinetic Term” that effectively becomes “nonpolynomial” (or in Bekenstein and Milgrom’s terminology, “Aquadratic”) once the auxiliary nondynamical scalar field has been algebraically eliminated from the theory in favor of the metric and vector fields.
What Skordis and Zlosnik have done in arXiv:2007.00082 is find an alternative Tensor-Vector theory in which light and gravitational waves are guaranteed to propagate at the same speed, and also spatial variations in the “Vector” field act enough like ersatz “Dark Matter” to closely reproduce the peaks in the CMB power-spectrum. (Albeit, the vector field does not act _exactly_ like DM — see their “nonstandard pressure term” (16).)
It’s also interesting to note that Skordis & Zlosnik theory exhibits a “shift symmetry” in one of the scalars, i.e. their lagrangian (10) is unchanged if a constant is added to one of the auxiliary fields. Such “shift symmetries” also appear in effective field-theories of “superfluids” (see e.g. arXiv:1108.2513), so perhaps the Skordis & Zlosnik theory can be reformulated as a “Superfluid Dark Matter” theory in the same spirit as Khoury et al or Hossenfelder & Mistele, in which the “MOND Force” arises due to the exchange of “virtual phonons” within the superfluid phase.
LikeLike
Definitely, a very interesting result!
Thanks for keeping us up to date with all these interesting developments.
As far as I understand, it’s not a complete theory; it’s a “class of theories” (or a “framework theory”) which fulfills the basic requirements (consistency with GR, correct speed of gravitational waves, etc) and can give exactly the same results as ΛCDM (for the CMB spectrum).
So, I think it’s a “step on a longer path” – but at least now a new path is available!
LikeLiked by 1 person
Yes, definitely not a final answer – or necessarily even a correct step. More a demonstration that it can happen in such a way, not that it must.
LikeLiked by 1 person
Stacy,
MOND vs CDM is fascinating. Your blog has become my site for the latest information and I check it almost daily for a new release. Thank you. From my reading of the literature I have 4 questions that I have not seen answered previously and I am hoping that you will take the time to address them.
The first three are related to gravitational lensing:
I gather that lensing is, in general, consistent with CDM. Does lensing provide accurate enough measurements that one can state that the rotational curves and lensing provide nearly identical estimates of the amount and location of the CDM?
Obviously, for MOND to explain lensing, something dramatically different then the rotational assumption must be added. I understand that theories such as TeVeS are consistent with the lensing observations. Can you provide a sort of layman’s explanation of how this is brought about? For example, does it follow naturally from the acceleration assumption, or is it necessary to add completely new “fudge factor(s)” to get the correct bending of light?
Related to this, is it correct that TeVeS is definitively ruled out by the gravity wave observations that gravity and light waves have the same velocity?
Finally, one of main promises of the Gaia satellite was that detailed measurements of individual stars in the Milky Way would provide an order of magnitude improvement in estimates of the location, etc. of CDM and, possibly, distinguish between CDM and MOND. There have now been two releases of Gaia data. What is the status of these promises?
LikeLike
That’s a lot to address in a post, let alone here. TeVeS (and now RelMOND) give equivalent conventional signals to both kinematics and lensing. This comes about by permitting a difference between the Einstein and physical metrics, which determine the trajectories do the photons follow – the one that knows about the modification or not. It is a lot easier to write theories where lensing does not receive a boost, but these are all excluded by the observations. So it isn’t necessary to add a new fudge so much as it is to get the fudge one has already added to apply to lensing.
The equivalence of the speed of light and gravitational waves excludes all theories that break this, but theories that break this were already suspect. TeVeS, like MOND, is a family of possible theories, so the already dubious flavors are excluded.
Gaia data are TMI – too much information. It will take longer to analyze than to collect. So far, there are indications in both directions. The rotation curve of stars is now consistent with that of interstellar gas is consistent with MOND, but only if you do it right: features we traditionally ignore or assume are smooth (e.g., bumps in the density distribution due to spiral arms) can no longer be ignored. This makes the analysis more complex. Same for the vertical restoring force, which is something that troubles me greatly in MOND, albeit at the 30% level. There are indications in the Gaia data of various ringing and breathing and other oscillatory modes, so it is going to be challenging to sort out the equilibrium potential from transient effects. In principle, Gaia should also provide a test with widely separated binaries, which (depending where they are in the Galaxy) should have a MONDian boost to their orbital velocities but shouldn’t survive at all in CDM because of disruption by subhalos.
So yes, Gaia data are great, and should help a lot. But the first thing one always learns with major advances like this is that there are lots of inconvenient details that you can no longer ignore.
LikeLike
What is the remaining 70% which troubles you in MOND – except of the fact that there is no complete relativistic MOND theory yet available – clusters and CMB?
LikeLike
I didn’t say 70% troubled me. I said the vertical force in the Milky Way troubles me for being about 30% off – an amount that we would be excited about if a dark matter theory could make a prediction that got so close.
LikeLike
Is it 30% too high or 30% too low? Does it get worse at greater elevations relative to the disk?
LikeLike
By my analysis, MOND seems to over-predict the vertical force. The *shape* is right – the variation of K(z) is precisely predicted, but with an offset.
Despite all the existing work, I think it remains early days for this problem, in terms of both the data and its analysis. Many qualitative predictions of MOND are apparent in the data, but quantitatively the vertical force doesn’t seem to match up (at this ~30% level) with the radial force.
LikeLike
Ah, okay, thanks for clarifying!
This discrepancy is a very interesting point (I have never heard about it before).
So, MOND is 30% off.
What about DM – or DM does not account for it at all?
I have found this paper of yours:
https://iopscience.iop.org/article/10.3847/0004-637X/816/1/42
Is it a good starting point to understand the vertical force discrepancy, or you could suggest some other link?
LikeLike
Yes, that’s a good starting point. It isn’t an endpoint, because I’d publish that if I understood this problem.
So for DM, the vertical force looks right in this specific analysis, but only once you spot it MOND in the radial direction. That’s sorta like the college football playoff system: we’ll just put start you off with 3/4 of the field already behind you; let’s see if you can at least kick a field goal from here. I discuss this conundrum in the paper you cite. Do not have a good answer for it.
LikeLike
Great, thanks a lot!
LikeLike
MOND can well be an effective theory in a four dimmensional brane, of matter distribution in a fifth dimmensional bulk. Thus, GR and (dark) matter in 5 dimmensions lead to a MOND in our 4d world. That would explain why dark matter can only be observed via gravity.
LikeLike
MOND is certainly an effective theory of something, and we should take advantage of it as such in developing deeper theory. Most development in terms of DM aggressively ignores and actively denies this simple fact.
LikeLike
Congratulations on your latest preprint. https://arxiv.org/abs/2007.08610
LikeLiked by 1 person
Stacy, the action (10) from the paper is really ugly! It introduces new fields (it is not clear to me how many) and many additional terms to the Hilbert action of general relativity. It takes long to understand the new terms. They also introduce at least one new constant of nature (K_B).
Any idea to increase gravity to more than 1/r^2 at large distances must have a good motivation. The paper is more a proof that one can imagine such an option. But whether one introduces a new field or whether one introduces dark matter seems not so different to me, conceptually. (I hope that I do not misrepresent the paper).
But what is now needed is an argument why the gravitational attraction is stronger at large distances. Verlinde might be right that it is an effect of the cosmological horizon. To me the real question is thus: Does the horizon increase 1/r^2 gravity?
If we can answer yes, MOND follows.
LikeLike
Gravity is definitely observed to be stronger than inverse square in low acceleration systems. That’s why we invoke dark matter or attempt modifications like MOND. These are both conceptually different (perhaps the otherwise wonderful formulation of theories in terms of actions does us a disservice in this regard?) and practically different. Dark matter plus baryons could result in an arbitrary set of combinations with no guarantee that seeing just one component would enable prediction of the other. Modifications like MOND lead to a unique relation between the baryon distribution and the resultant force. The latter is what is observed in galaxies.
LikeLike
@Gianni, the Skordis & Zlosnik RelMOND lagrangian, while complex, actually depends only on the physical metric and the vector field $B_\mu$, see the discussion in the paragraph beginning just before Eqn. (5).
The auxiliary fields Skordis & Zlosnik somewhat confusingly denoted as $\mu$ and $\nu$ (which letters are also used as tensor indices) are “nondynamical” fields that can be reexpressed in terms of the metric and the vector field $B_\mu$, and were introduced only to simplify the lagrangian; they are later eliminated (“integrated out”, see the discussion after Eqn. (9)) to yield the lagrangian (10). (The “nondynamical” auxiliary metric and the scalar field $\sigma$ in Bekenstein’s “TeVeS” can likewise both be algebraically eliminated in terms of the physical metric and Bekenstein’s vector field, as shown in Zlosnik, Ferreira, and Starkman’s arXiv:gr-qc/0606039, yielding a lagrangian that is just as complex as Skordis & Zlosnik’s lagrangian, and in fact is in the same family of “Generalized Tensor-Vector Gravity” lagrangians as Skordisdis & Zlosnik’s lagrangian.)
The “fields” $\mathcal{Y}$ and $\mathcal{Q}$ are likewise “auxiliary fields”; they are merely shorthand notations for a pair of somewhat complex scalar invariants constructed from the physical metric, the vector field $B_\mu$, and its first derivatives.
The coupling constant $K_B$ is dimensionless, and the presence of a new constant of nature in any theory that reduces to MOND should hardly be surprising, because MOND likewise introduces a new constant of nature, the “Critical Acceleration” $a_0$. In this respect the Skordis & Zlosnik lagrangian is also an advance, since they have succeeded in replacing Milgrom’s dimensionful constant $a_0$ whose order of magnitude satisfies several mysterious “cosmological coincidences” with a dimensionless constant; — and now in their model, Milgrom’s “cosmological coincidences” are finally explained as an effect of the background FLRW cosmology, just as Milgrom had conjectured.
So now that Skordis & Zlosnik hav found a “proof of principle” lagrangian that overcomes the objections against TeVeS, the question becomes whether there is a simpler theory that has the same favorable properties as Skordis & Zlosnik’s lagrangian.
LikeLike
Hello Stacy! First, thank you very much for this another excellent addition. I wanted to react about one of your statements, I quote:
“I think that the assumption that General Relativity is correct is indeed an excellent one. It has repeatedly passed many experimental and observational tests too numerous to elaborate here.”
I think that the correct and accurate scientific assessment of GR is, in all truthfulness and honesty, a little bit more bleak than what you wrote here. It is correct to say that GR has successfully passed a number of tests, but unfortunately, it is also correct to say that it DIDN’T pass other cohorts of very important tests.
As a theory of gravity, GR does not pass the test of stellar dynamics at galactic and cluster scales ( where it clearly and unambiguously predicts Newton law for gravity), and as a theory of “space-time” dynamics that serves as the backbone of our concordant model of cosmology, it didn’t pass the test for the homogeneity of the CMB ( it clearly predicted inhomogeneous CMB) nor the test of “space-time” accelerating expansion rate ( it predicted a decelerating expansion). We witnessed how this 3 major fails for GR brought 3 new major hypothesis about the inner workings of our universe, hypothesis that introduces objects/concepts that remain of unknown/unproven nature up to these days, namely Dark matter, Dark energy and cosmic inflation ( in all their variations). You can add to the mix another number of troubling tensions that GR brings to physics: It appears to be incompatible with quantum mechanics at a very fundamental level and violates unitary ( leading to the infamous “information paradox”). All in all, it seems that a good bunch of major physics conundrum of our time (at least in astro-particle physics and cosmology) are converging towards GR shortcomings.
My (unorthodox) opinion is thus that the assumption that GR is correct is not an excellent one as it has failed very important observational tests and brought, for its preservation as a correct physical theory of gravity, many problems that are still unresolved up to these days. I would tend to be of the opinion that as long that dark matter hypothesis remains unproven, dark energy remains unexplained etc…that GR is indeed falsified as the burden of the proof (dark matter/dark energy/inflation etc…) remains on her shoulder in order to survive, so as to speak.
In the light of that frame of mind, I find it peculiar that it seems to be compulsory that every attempt to solve these major problems has to “conform” to GR “space-time” formalism, be “relativistic” friendly, as it seems that, on the contrary, every alternative attempt paving roads to success are exhibiting major tensions with GR postulates, be it compatibility with equivalence principle and/or necessity to reintroduce a privileged frame of reference ( Ether theories). In that sense, I think that it is not that far fetched to envision the very real possibility that GR is indeed “ontologically” incorrect, that it’s very essence, as a theory of space-time, is not in tune with the reality and/or the inner workings of our physical universe.
This lead to the general impression that having to make alternative attempts “relativistic” is akin to some sort of branding, a buzzword that helps in getting the attention of the wider scientific community that remains so reluctant to admit that anything not “relativistic” can possibly describe our world, even if at their core these attempts violate every core principle of “relativistic” physics. It emphasizes more strongly than ever the social constructs that permeates the scientific communities in search of validation from one each other.
LikeLike
The challenge, of course, is to retain the successful portions of GR while building a theory that also explains these new phenomena. So I think starting with a relativistic theory is natural in terms of building-from-what-we-know. Indeed, many theorists have expressed discomfort to me about theories (like pure MOND) that are not generally covariant, as they take that as a necessary prerequisite. I find this standard a bit high, as Newtonian dynamics does not count as a valid theory by this standard. What you suggest is a step beyond, which may well be required… it seems to me that we are missing some fundamental principle. Einstein is said to have worked hard to include Mach’s principle in GR, but ultimately gave up, so one can at least imagine an conceptual generalization of inertia (for example) that might lead to an ontologically different perception of how things work, just as GR changed Newton while also incorporating his successes. If so, it seems we are far from achieving such a theory, as barely anyone is taking it seriously, much less working on it.
LikeLike
I have just read Lyman Page’s “the Little Book of Cosmology”, published earlier this year by Princeton University Press. While, obviously, it isn’t MONDian I think it explains the Standard Model of Cosmology very well for the non-specialist and also covers how measurements of different properties of the CMB, particularly polarization, can give us further information.
LikeLike
Quick question. I’m wondering if the new RelMOND theory can be used to infer Hubble’s constant from the microwave background, much like GR is used by cosmologists to infer H0. If so, I’d be fascinated to see if the estimate agrees with what astronomers infer from the nearby universe. The Hubble tension might disappear …
LikeLike
I also wonder that. I asked the authors many questions, of which this was one. They basically said “maybe.” Obviously there is still a lot to explore, and it will take some time to do so. I also asked about the effect of the baryon density, which they say doesn’t matter. This is consistent with my experience, which I hope to post something about soon. So the tension in BBN (often called the lithium problem in an abundance of confirmation bias, because it couldn’t possibly be a problem with the interpretation of the CMB) goes away, with the Hubble tension TBD.
LikeLiked by 1 person
Was another of your questions about structure formation?
Can RelMoND be used to make a portrait of the early universe? I know that MoND builds structure too quickly, I wonder how RelMoND compares to this.
LikeLike
Pure MOND builds structure quickly. Whether it does so too quickly depends on what aspect of structure formation you’re talking about. The earliest MOND calculations overshot sigma_8 at z=0 by a factor of 2. That’s a fair sight better than the earliest conventional calculations, which were off by over a factor of 100. Hence the need to invoke dark matter, and later, to invoke exactly the right amount of dark matter to get it just right. (Remember that the COBE detection of power on large scales was unexpectedly high for its time.) One tension is LCDM is that there seems to be too little DM/power to form the earliest structures observed at high redshift, which MOND’s quickness does naturally.
As for RelMOND, I hesitate to speak too much for the authors. But yes, I asked that, and the answer was that they get the power spectrum right, just couldn’t fit it all in one paper.
LikeLike
The opportunity for circular reasoning is apparent – and frequently indulged.
Generally speaking, circular reasoning is the only way to justify LCDM’s invocation of numerous, unobservable, entities and events. The model can be said to agree with observations only to the extent that LCDM is allowed to invoke the existence of things that cannot be observed. So, the reasoning goes:
1. LCDM is a correct description of reality – it agrees with observations
2. Therefore, the unobserved entities and events required by LCDM, in order to agree with observations, must exist because…
3. LCDM is a correct description of reality – it agrees with observations
Superficially, the problem appears to lie with General Relativity, but in reality it is both a conceptual, and an over-simplification problem, within the standard cosmological model. Conceptually, it is oxymoronic to apply the field equations of GR to the universal FLRW metric. GR was conceived in the absence of such a universal frame. A universal frame obviates the need for GR.
It is also, grossly inappropriate to treat multi-body, distributed-mass systems with point-mass analysis. On the scale of galaxies and galaxy clusters, point-mass analysis simply does not work. It unfailingly gives incorrect expectation values for physical systems that are significantly more complex than the mathematical formalisms, designed for the Solar System, allow for.
The circular reasoning supporting CDM, the ad hoc, all-purpose patch to any gravitational modeling difficulties, is of a piece with that supporting the LCDM model. Circular reasoning is a logical fallacy; it is never appropriate, and yet its usage is widespread in theoretical physics. How this came to be will provide much grist for the paper mills of future historians of science.
As far as MOND goes, it is superior to CDM partly because it has predicted subsequently observed phenomena and because it does not posit the existence of physical things that cannot be detected. But MOND is dissatisfying because it is just math; it offers a useful calculational tool, without offering any physical explanation for why the tool works. The same can be said of RelMOND, I assume (no time to read the paper yet).
And this brings us back to a previous discussion about whether making correct predictions is necessary and sufficient to establish a scientific model. I would argue that a theoretical model that offers only a successful calculation method, while providing no physical explanation for why the tool works, is at best scientifically incomplete.
At this juncture, there are two options. One is to seek a theory that might work, and develop it to the point where it can be tested.
Yes, but … The methodology one uses to seek a theory is critical to a scientifically successful outcome. If the seeking takes place entirely within math-space, without reference to the physical system (other than to the desired outcome) that is being modeled, the results will be less than satisfactory, even if the model can be said to “work”. If there is no understanding of why the math works then the scientific task is incomplete.
It could be argued that both the Newtonian and GR gravitational models already lack explanatory power for the gravitational mechanism (unless you accept the modern conceit of a substantival spacetime, one for which there is no empirical evidence). This is true, but not exculpatory. It should be a priority of theoretical physics to understand the physical cause of the gravitational effect our models correctly (and incorrectly) calculate. That such an effort does not appear to be even an afterthought in the scientific community is, in itself, scandalous.
LikeLike
budrap,
As you say, it is the physical cause of gravity that should be a priority for theoretical research. All methods that I can see invent new concepts such as gravitons and/or dark matter, for which there is zero experimental evidence. What is wrong with trying to develop a theory that works with the particles that we already know exist? Then it becomes obvious that gravity is caused by neutrinos, because (a) there is no other particle that could do the job, and (b) neutrinos *do* cause effects at huge distances across the universe, and if these effects are not gravity, then what are they? Physicists will not listen to this argument, because they have been indoctrinated with the catechism that force mediators must be bosons. Absolute nonsense. The only requirement for a mediator for gravity is that it should be massless. Everything else is sheer prejudice.
LikeLike
@Robert A. Wilson, the reason for this “prejudice” is called the “Pauli Exclusion Principle”. Fermion exchange cannot build up to produce macroscopic long-range forces (unless the fermions undergo “bose-einstein condensation” into effective bosons) because at most one fermion can be in any given quantum state — even when the exchanged fermions are “virtual particles”. “No-Go” theorems on macroscopic-fermion-mediated forces go back at least as far as the very general S-matrix theorems on “soft particle exchange” by Steven Weinberg in the mid-1960s, see e.g the references in arXiv:1209.4876. By contrast, it is not only possible to pack many virtual bosons into the same quantum state in order to build up a macroscopic force, but it is even favorable for bosons to do so.
Also, perhaps you have not yet noticed, but the experimental confirmation of “neutrino oscillations” in 1998 at the Super-Kamiokande detector and subsequent observations by SNO in Canada and elsewhere means that neutrinos are now known to have nonzero masses. So if you are depending on neutrinos being “massless”, you are more than 20 years out of date.
Click to access rpp2018-rev-neutrino-mixing.pdf
LikeLike
Gah, I did not say that well, I should never post before coffee. 😦
If there is some form of “pairing force” between fermions, e.g. as in the BCS theory of superconductivity, the fermions can pair up into effective bosons — and it is these effective bosons that can then condense into a BEC that can exert macroscopic effective forces. But note that the fermions must be massive in order to pair up and condense, and that these fermion pairs will themselves be massive.
LikeLike
Well, I am not sure I entirely agree. First of all the belief that neutrinos have non-zero mass is a most egregious example of the triumph of circular reasoning over common sense. I am not 20 years out of date, I simply refuse to accept an argument that says: A implies B, therefore B implies A. The Pauli exclusion principle for massless fermions travelling at the speed of light is a little more difficult to defend than the same principle for massive particles. I have discussed these ideas at length and in depth with a serious expert in superconductivity, and he sees no obstacle to what I propose. Doubtless I have not got everything right, and you can certainly pick holes in my argument. But at least my model is internally consistent, which is more than can be said for the standard model.
LikeLike
Except that a new IR scale for neutrinos is well studied in the condensate approach by, for instance, Alexander or Dvali-Funcke, whose Two Chern-Simons model may be connected to categorical axioms in a condensed matter formalism. The Pauli exclusion principle now belongs to the quantum information prior to the emergence of spacetime (via universal quantum computation) and there exists a new supersymmetry between neutrinos and photons, requiring only SM states and no DM.
LikeLike
Thanks for providing this forum, Stacy.
And congratulations on your latest paper about the EFE!
How will the LCDM apologists wriggle out of that?
I guess this topic won’t get “stale” for a long time,
so I would like to offer a few comments and questions
arising from my desperate efforts to understand this
exciting paper by Skordis & Złośnik (K&Z).
— Their ingenious solution to the problem of GW propagation
at luminal velocity was actually published last year [ref 73].
They apparently even proved identical Shapiro delays as the
two signals snake their way around the gravitational wells in
a modern evolved universe, which I guess was a first.
— I think most other ingredients in this new comprehensive
treatment had been introduced by others. For example, the same
shift-independent “k-essence” scalar field proposed by Scherrer
[ref 61] had already been shown in 2005 by Giannakis & Hu
(astro-ph/0501423) to provide similarly good agreement with
the CMB, without any help from a vector field. (See their Fig. 2.)
What seems most exciting about this K&S paper is that they
simultaneously address all other requirements in a coherent
comprehensive treatment.
— Except possibly one “elephant in the room”?
(Please tell me what I’m missing here.)
In Bekenstein’s original 2005 presentation of TeVES
(astro-ph/0403694), in the last paragraph of Section E,
we find the word “embarrassment”, referring to the
“cosmological matter problem”. In the absence of dark matter,
how does one find enough matter/energy for the critical density
to produce the current value of the Hubble parameter H0 ,
and a flat universe? Of course, the MOND force enhancement
helps, but apparently it wasn’t enough in TeVeS. Or was it too
much in some sense, resulting in a Hamiltonian that was
“unbounded from below”? (Is that problem now solved?)
I suppose that one can’t increase the dark energy density
without also getting too much “Dark Suction” (negative pressure)
to match the alleged acceleration. (Yes, Dark Energy sucks!)
— K&S show on the rhs of page 3, “cosmological observables”,
that the average scalar field density is unconstrained in the context
of linear perturbations, depending on the integration constant I0.
So one can choose a scalar energy density large enough for H0 ,
but wouldn’t it inevitable collapse into the galactic halos that would
obviate the MOND force enhancement? The sound velocity of the
scalar field seems too small to prevent that. (K&S even call it dust.)
Also, doesn’t the average scalar field density have to be large
enough to avoid going negative in the voids created by the nonlinear
evolution to produce the MPS? This all seems like the familiar
“rock and a hard place”. Are halos inevitable? As you said, Stacy,
that would (also) suck. I hope the next K&S paper addresses
these issues more explicitly.
— I understand from that paragraph that the vector field doesn’t
affect the Friedmann equations for an isotropic homogenous
universe, which are said to be still “satisfied”. (But the vector
field is later shown to become intimately involved in the linear
perturbations of the scalar pressure affecting the CMB.)
So can we still write 𝜌_crit = 3H0^2/(8πG)? Using which G?
We are told G_hat = 2∙G_tilde/(2-K_B) and G_N = (1+1/𝜆s)G_tilde .
— Is relMOND intended to include the External Field Effect?
I guess that’s (more than) enough for now!
LikeLiked by 1 person
Wow! Lots of great questions, most of which I cannot answer. To start at the end, I don’t see how an EFE is avoidable in RelMOND, but I haven’t gone through the maths. Nor is it obvious to me that we can write a meaningful expression for the critical density. This might be a good thing. One of the things that made me stop and think early on, and it still does, is that the effective potential in straight MOND is logarithmic. So there is no such thing as an unbound universe. Everything will eventually recollapse no matter the density – eventually the force law wins. This is a natural solution to the flatness/coincidence problem that launched Inflation. The density is just a number; there is no special critical value to compare it to. Of course, that’s in the absence of dark energy, so who knows how that folds into it. Once we have it, I think that one could get away with turning up Lambda to closer to de Sitter with respect to many observations; some observations even imply just this (see my post on EDGES). What troubles me most about this approach is that it makes the universe a lot older than it seems to be (~20 vs 13 or 14 Gyr). Something that strikes me about the current model is that the age of the LCDM universe is very close to the Hubble time, 1/H0. So we live at a very peculiar time after deceleration before too much acceleration so that this is just so. Maybe the expansion is just coasting? That is also good with a lot of observational data. Where it collapses utterly is against the geometry: q0=0 is a decent fit to things like the Type Ia SN data but completely impossible in terms of the CMB. So maybe, in some underlying theory, the traditional connection between geometry and expansion history is broken? Or at least different. Lots to ponder, as you say.
LikeLiked by 1 person
Ok, now I wonder if Dark Energy could be a crude solution to the “embarrassing” problem, if one adjusted its equation of state to compensate the effect on the acceleration while increasing its energy density. Is there something sacred about 𝜔 = -1?
LikeLike
Yes and no. People have certainly considered other value, but observational constraints claim it has to be very close to w = -1. Whether those still hold in the context of RelMOND would have to be reevaluated.
LikeLike
I am still concerned about how this theory addresses galaxy clusters like the Bullet, but other virialized galaxy clusters as well. In addition, based on a brief email exchange with Skordis, the advice I got is that the large scale structure and expansion history are the same as in LCDM. If so, our paper on the KBC void and Hubble tension (described in the next post and Arxiv 2009.11292) suggests that the RelMOND theory of Skordis & Zlosnik (2020) is also ruled out. However, if large scale structure is enhanced by just a factor of a few over standard expectations on a 300 Mpc scale, it would be enough – if the galaxy cluster problems can be addressed. I suppose these are the sorts of issues that Skordis and collaborators are considering.
LikeLiked by 1 person
I think RelMOND is an important advance, not necessarily the final destination. As you say, they seem focused on exactly reproducing LCDM, which is necessary to show is possible. That opens the door to consider models beyond that, in the ways you described and others (e.g., the expansion history during the Dark Ages as probed by experiments like EDGES). Gotta walk before you can fly.
LikeLiked by 1 person
I disagree that it is necessary to show that a theory can reproduce LCDM. It might be necessary to reproduce the empirical successes of LCDM, but then really what is being reproduced are the observations. And these do indicate the presence of the void, which is incompatible with LCDM in the linear regime. So reproducing LCDM in the sense of having the same structure growth in the linear regime will lead to a major disagreement with local observations. I hope this was not the primary motivation for RelMOND.
LikeLike