I haven’t written much here of late. This is mostly because I have been busy, but also because I have been actively refraining from venting about some of the sillier things being said in the scientific literature. I went into science to get away from the human proclivity for what is nowadays called “fake news,” but we scientists are human too, and are not immune from the same self-deception one sees so frequently exercised in other venues.
So let’s talk about something positive. Current grad student Pengfei Li recently published a paper on the halo mass function. What is that and why should we care?
One of the fundamental predictions of the current cosmological paradigm, ΛCDM, is that dark matter clumps into halos. Cosmological parameters are known with sufficient precision that we have a very good idea of how many of these halos there ought to be. Their number per unit volume as a function of mass (so many big halos, so many more small halos) is called the halo mass function.
An important test of the paradigm is thus to measure the halo mass function. Does the predicted number match the observed number? This is hard to do, since dark matter halos are invisible! So how do we go about it?
Galaxies are thought to form within dark matter halos. Indeed, that’s kinda the whole point of the ΛCDM galaxy formation paradigm. So by counting galaxies, we should be able to count dark matter halos. Counting galaxies was an obvious task long before we thought there was dark matter, so this should be straightforward: all one needs is the measured galaxy luminosity function – the number density of galaxies as a function of how bright they are, or equivalently, how many stars they are made of (their stellar mass). Unfortunately, this goes tragically wrong.

This figure shows a comparison of the observed stellar mass function of galaxies and the predicted halo mass function. It is from a recent review, but it illustrates a problem that goes back as long as I can remember. We extragalactic astronomers spent all of the ’90s obsessing over this problem. [I briefly thought that I had solved this problem, but I was wrong.] The observed luminosity function is nearly flat while the predicted halo mass function is steep. Consequently, there should be lots and lots of faint galaxies for every bright one, but instead there are relatively few. This discrepancy becomes progressively more severe to lower masses, with the predicted number of halos being off by a factor of many thousands for the faintest galaxies. The problem is most severe in the Local Group, where the faintest dwarf galaxies are known. Locally it is called the missing satellite problem, but this is just a special case of a more general problem that pervades the entire universe.
Indeed, the small number of low mass objects is just one part of the problem. There are also too few galaxies at large masses. Even where the observed and predicted numbers come closest, around the scale of the Milky Way, they still miss by a large factor (this being a log-log plot, even small offsets are substantial). If we had assigned “explain the observed galaxy luminosity function” as a homework problem and the students had returned as an answer a line that had the wrong shape at both ends and at no point intersected the data, we would flunk them. This is, in effect, what theorists have been doing for the past thirty years. Rather than entertain the obvious interpretation that the theory is wrong, they offer more elaborate interpretations.
Faced with the choice between changing one’s mind and proving that there is no need to do so, almost everybody gets busy on the proof.
J. K. Galbraith
Theorists persist because this is what CDM predicts, with or without Λ, and we need cold dark matter for independent reasons. If we are unwilling to contemplate that ΛCDM might be wrong, then we are obliged to pound the square peg into the round hole, and bend the halo mass function into the observed luminosity function. This transformation is believed to take place as a result of a variety of complex feedback effects, all of which are real and few of which are likely to have the physical effects that are required to solve this problem. That’s way beyond the scope of this post; all we need to know here is that this is the “physics” behind the transformation that leads to what is currently called Abundance Matching.
Abundance matching boils down to drawing horizontal lines in the above figure, thus matching galaxies with dark matter halos with equal number density (abundance). So, just reading off the graph, a galaxy of stellar mass M* = 108 M☉ resides in a dark matter halo of 1011 M☉, one like the Milky Way with M* = 5 x 1010 M☉ resides in a 1012 M☉ halo, and a giant galaxy with M* = 1012 M☉ is the “central” galaxy of a cluster of galaxies with a halo mass of several 1014 M☉. And so on. In effect, we abandon the obvious and long-held assumption that the mass in stars should be simply proportional to that in dark matter, and replace it with a rolling fudge factor that maps what we see to what we predict. The rolling fudge factor that follows from abundance matching is called the stellar mass–halo mass relation. Many of the discussions of feedback effects in the literature amount to a post hoc justification for this multiplication of forms of feedback.
This is a lengthy but insufficient introduction to a complicated subject. We wanted to get away from this, and test the halo mass function more directly. We do so by use of the velocity function rather than the stellar mass function.
The velocity function is the number density of galaxies as a function of how fast they rotate. It is less widely used than the luminosity function, because there is less data: one needs to measure the rotation speed, which is harder to obtain than the luminosity. Nevertheless, it has been done, as with this measurement from the HIPASS survey:

The idea here is that the flat rotation speed is the hallmark of a dark matter halo, providing a dynamical constraint on its mass. This should make for a cleaner measurement of the halo mass function. This turns out to be true, but it isn’t as clean as we’d like.
Those of you who are paying attention will note that the velocity function Martin Zwaan measured has the same basic morphology as the stellar mass function: approximately flat at low masses, with a steep cut off at high masses. This looks no more like the halo mass function than the galaxy luminosity function did. So how does this help?
To measure the velocity function, one has to use some readily obtained measure of the rotation speed like the line-width of the 21cm line. This, in itself, is not a very good measurement of the halo mass. So what Pengfei did was to fit dark matter halo models to galaxies of the SPARC sample for which we have good rotation curves. Thanks to the work of Federico Lelli, we also have an empirical relation between line-width and the flat rotation velocity. Together, these provide a connection between the line-width and halo mass:

Once we have the mass-line width relation, we can assign a halo mass to every galaxy in the HIPASS survey and recompute the distribution function. But now we have not the velocity function, but the halo mass function. We’ve skipped the conversion of light to stellar mass to total mass and used the dynamics to skip straight to the halo mass function:
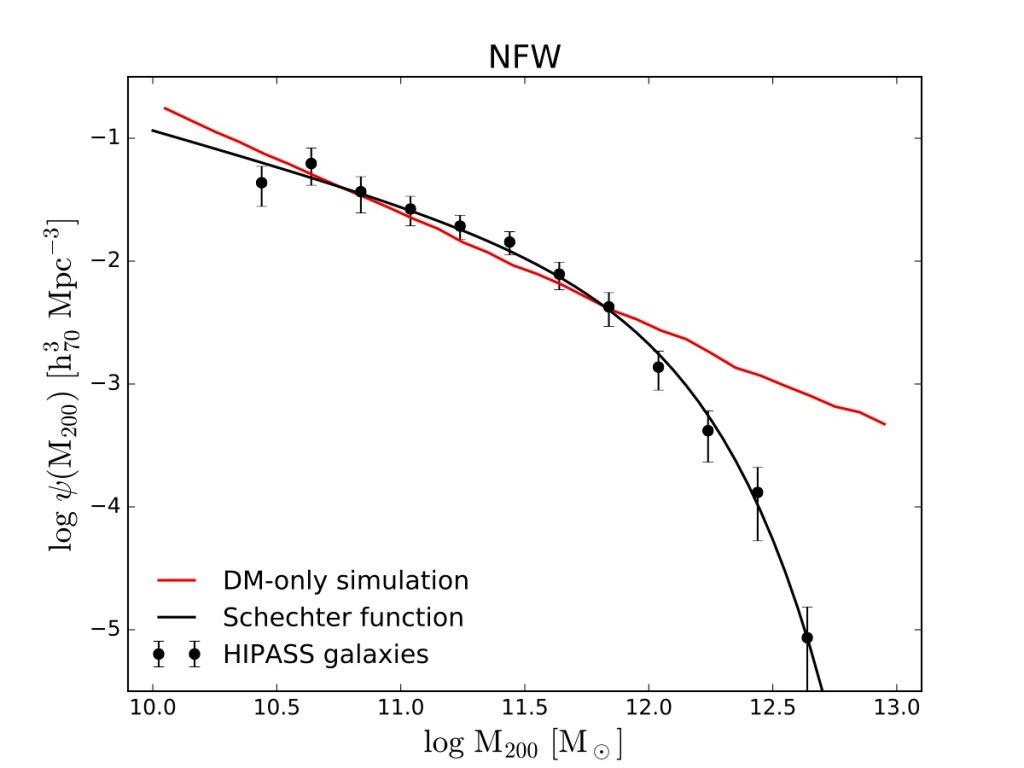
The observed mass function agrees with the predicted one! Test successful! Well, mostly. Let’s think through the various aspects here.
First, the normalization is about right. It does not have the offset seen in the first figure. As it should not – we’ve gone straight to the halo mass in this exercise, and not used the luminosity as an intermediary proxy. So that is a genuine success. It didn’t have to work out this well, and would not do so in a very different cosmology (like SCDM).
Second, it breaks down at high mass. The data shows the usual Schechter cut-off at high mass, while the predicted number of dark matter halos continues as an unabated power law. This might be OK if high mass dark matter halos contain little neutral hydrogen. If this is the case, they will be invisible to HIPASS, the 21cm survey on which this is based. One expects this, to a certain extent: the most massive galaxies tend to be gas-poor ellipticals. That helps, but only by shifting the turn-down to slightly higher mass. It is still there, so the discrepancy is not entirely cured. At some point, we’re talking about large dark matter halos that are groups or even rich clusters of galaxies, not individual galaxies. Still, those have HI in them, so it is not like they’re invisible. Worse, examining detailed simulations that include feedback effects, there do seem to be more predicted high-mass halos that should have been detected than actually are. This is a potential missing gas-rich galaxy problem at the high mass end where galaxies are easy to detect. However, the simulations currently available to us do not provide the information we need to clearly make this determination. They don’t look right, so far as we can tell, but it isn’t clear enough to make a definitive statement.
Finally, the faint-end slope is about right. That’s amazing. The problem we’ve struggled with for decades is that the observed slope is too flat. Here a steep slope just falls out. It agrees with the ΛCDM down to the lowest mass bin. If there is a missing satellite-type problem here, it is at lower masses than we probe.
That sounds great, and it is. But before we get too excited, I hope you noticed that the velocity function from the same survey is flat like the luminosity function. So why is the halo mass function steep?
When we fit rotation curves, we impose various priors. That’s statistics talk for a way of keeping parameters within reasonable bounds. For example, we have a pretty good idea of what the mass-to-light ratio of a stellar population should be. We can therefore impose as a prior that the fit return something within the bounds of reason.
One of the priors we imposed on the rotation curve fits was that they be consistent with the stellar mass-halo mass relation. Abundance matching is now part and parcel of ΛCDM, so it made sense to apply it as a prior. The total mass of a dark matter halo is an entirely notional quantity; rotation curves (and other tracers) pretty much never extend far enough to measure this. So abundance matching is great for imposing sense on a parameter that is otherwise ill-constrained. In this case, it means that what is driving the slope of the halo mass function is a prior that builds-in the right slope. That’s not wrong, but neither is it an independent test. So while the observationally constrained halo mass function is consistent with the predictions of ΛCDM; we have not corroborated the prediction with independent data. What we really need at low mass is some way to constrain the total mass of small galaxies out to much larger radii that currently available. That will keep us busy for some time to come.
Pretty interesting. I am not sure how to process all this, it involves several aspects of Galactic Astronomy that I am not as familiar with as I would like to be, however I am very glad to see you posting again. You have definitely given me a new topic (sub topic) to read up on.
LikeLike
Fascinating, and although not a physicist I feel that I understand most of this. My favourite bit? “The rolling fudge factor that follows from abundance matching is called the stellar mass–halo mass relation.” Please do keep sharing. I was also amused that you couldn’t help but have another pop at SCDM.
LikeLike
LCDM is the SCDM of today – a theory every one believes must be true, but could prove to be badly misleading. So yes, I always take the opportunity to remind people of this analogy, especially at I notice many younger scientists are blissfully unaware that we’ve been down this path before.
LikeLike
Stacy,
a straight question: do you believe in Lambda, i.e., in dark energy?
As you know, several research groups question its reality, as done, e.g., by the various papers of Sarkar, Tsagas, Rameez, or Wilshire. They claim that Lambda is an artefact of either measurements or the peculiar situation of our solar system. (Their claim is vaguely similar to MOND’s claim that dark matter is an artefact of measurements – though the analogy is not really good.)
Best regards
Christoph
LikeLike
I believe the evidence that leads us to infer Lambda.
Lambda is a construct within the framework of General Relativity. It might be what it is, or it might be an indication that the theory is inadequate. In the latter case, one imagines there could be some more general theory in which it becomes clear what it really means… the underlying theory might deviate from GR in a way that “looks like” Lambda. So believing the evidence doesn’t compel belief in dark energy as an entity – that is one possibility, but not the only one.
If we restrict ourselves to the context of GR, the evidence for Lambda is overwhelming. I do not believe it can be an artifact of measurement error or our particular location. Attempts to dodge it usually involve dodging a single observation (e.g., Type Ia SN) while ignoring a host of other evidence (see https://tritonstation.com/2019/01/28/a-personal-recollection-of-how-we-learned-to-stop-worrying-and-love-the-lambda/).
LikeLike
IF, our universe is not alone in the cosmos. If the cosmos is much bigger / more massive and older than our Big Bang. Could Dark Energy just be the gravitational pull of the cosmos? I know this looks like just another crackpot idea but it is falsifiable and testable. It also resolves baryon asymmetry.
The universe has always been much bigger and older than we thought.
Hope I’m not abusing your blog. Keep writing.
LikeLike
You explanations here underscore how hard it can be for a layperson to understand what is really behind arguments for/against dark matter/energy. These statistical operations adjusting data may be well motivated, but it will not be apparent to the layperson that the close match of the “data” to predicted values is due to assumptions relating to the data adjustments.
I really value the work you put into this blog to give more context and nuance.
LikeLike
Frankly, many professionals have the same problem.
LikeLiked by 1 person
Have any good theories been proposed regarding why there appears to be a “soft” maximum galaxy size?
LikeLike
The predominant idea for this goes back to the mid-70s, and essentially says that the gas cooling time has to be shorter than the gravitational collapse time. Basically, there has to be time for the gas to collapse. This comes out to about the right upper mass limit for individual galaxies, but is rather crude in many respects – the cooling time is very sensitive to the metallicity of the gas; a spherical cow that ignores hierarchical substructure is assumed, and so on. Still, that’s the best I’ve heard.
LikeLike
FYI and FWIW, my blog post reacting to this post is found at: https://dispatchesfromturtleisland.blogspot.com/2020/01/cdm-predicts-wrong-mix-of-dark-matter.html
LikeLike
I know I should just look in the paper but did you guys do an experiment to see what happens as you relax that abundance matching prior? It would be nice to see a figure that somehow illustrates how the mass function is being “forced” to lcdm. Also, how come this prior is not forcing the high mass end to fit the simulation prediction?
LikeLike
Yes; hope to blog about that next, as Pengfei has a big paper coming out Soon. The short answer is that there is nothing in the kinematics that requires an abundance matching-like behavior, so left to itself, the faint end remains flat. At the bright end, one has to imagine that these very massive halos host groups and clusters, not individual galaxies, so the counting get screwy. Still, there is a problem with just calling the most massive galaxies the “centrals” of big groups, as many manifestly are not.
LikeLike
Stacy,
thank you for your clear answer. The cosmological constant indeed pops up in the Hilbert action of general relativity. How big is the modern measurement evidence that Lambda was constant over time not only over the last 100 million years, but also over the last 5 or more billion years?
(There are two backgrounds for the question: first, the theoretical papers on decaying Lambda scattered across the literature; secondly, most microscopic models about Lambda, such as emergent gravity, also suggest a decaying Lambda, with a value that was much higher in the early universe.)
Thank you for your wonderful blog. Please go on. Best regards, Christoph
LikeLike
Within the standard cosmology, the evidence for Lambda is strong. The evidence for time variable Lambda is not. People have certainly looked for such en effect, usually quantified as deviations of the dark energy equation of state from the nominal value for Lambda (P = -w*p where P is pressure, p energy density, and w = 1 for pure Lambda). The vast majority of such constraints find zero deviation: w = 1.0 plus or minus a small amount (< 0.1).
LikeLike
Thank you Stacy, but wouldn’t a slowly decaying Lambda (such as Lambda proportional to 1/R^2, R being the Hubble radius) still have w=1?
LikeLike
Lambda doesn’t decay. That’s the constant in cosmological constant.
LikeLike
Stacy,
thanks a lot for the interesting post.
At the end, what does it mean? Does it solve the missing satellite or dwarf galaxy problem? So the key idea, the rotation curves are not measured to far enough radii and the dark matter halos contain much more mass than so far assumed?
Thomas
LikeLike
It doesn’t solve the missing satellite problem; it just does not indicate one in the field, to the extent that we can measure. It has long been the problem that rotation curves (and most other tracers) don’t indicate where the edge of the dark matter halo is, so one is free to impose the “right” amount in the choice of priors (“right” in this context meaning what abundance matching wants).
LikeLike
Stacy,
thanks for the explanation, I am not so sure if I understood you correctly.
In a more general context, does the new findings/interpretation solves one of the pressing problems of ΛCDM? If it turnes out that the dark matter halos are much bigger than so far assumed, that they contain much more mass/dark matter, is that a new problem because for ΛCDM, since the angular distribution of the microwave background indicates that 20% of the total mass is baryonic? Or more directly, since you allways talk about dark matter halos, are you conviced that dark matter is indeed the cause of dynamics on galaxy scales?
Thomas
LikeLike
No. Yes. No.
This work does not solve any problem for LCDM, it only shows that these data are not necessarily in conflict with it at the low mass end.
It is correct to infer that the required halo masses vastly exceed what they should for the cosmic baryon fraction. This is not a new problem, at least not to me (https://tritonstation.com/2016/07/30/missing-baryons/). In effect, we have to have two forms of dark matter in every galaxy: non-baryonic cold dark matter AND dark baryons.
I am not at all convinced that dark matter is the cause of galaxy dynamics. But I do believe in objectivity, which involves seeing a problem from all sides. So I can put on a CDM hat and discuss that data in that context. That’s what one has to do to test a hypothesis – one needs to understand what it predicts, and not just knock down straw men.
LikeLiked by 1 person
Thanks a lot!
I think now I understand
Thomas
LikeLike
Not a scientist but love this blog. Surely it’s possible to directly constrain the halo mass by looking at galaxy mergers. A bigger halo would mean a faster closing velocity so if you looked at a population of mergers vs a model you could test this? Constructing the model sounds tricky for sure.
LikeLike
That is an excellent idea. It was examined by Dubinski et al a couple decades ago: https://arxiv.org/abs/astro-ph/9902217. What they found was that galaxy+halo models that made realistic-looking merger remnants needed to have progenitors with declining rotation curves. Those with realistically flat rotation curves did not make plausible merger remnants. That contradiction was briefly debated around the time, failed to penetrate the haze of cognitive dissonance, and has since been ignored.
As for closing velocity, yes, that depends on both the halo mass and the law of gravity. There is a limit as to how fast merging objects can fall together as they only have the age of the universe in which to accelerate. So even very massive things can only get up so much speed. The bullet cluster is one of the most massive objects in the universe, and yet its collision speed is considerably higher than the formal speed limit. In contrast, high-speed collisions turn out to be a natural consequence of MOND (https://arxiv.org/abs/0704.0381) – the longer effective range of gravity gets smaller masses up to a higher collision speed.
So yes, we should be able to test that with a population of merging objects. There are ongoing studies to look at this in galaxy clusters. The preliminary results I have seen suggest that high speed collisions are common, as predicted by MOND, but I rather doubt these will prove conclusive, as there are too many uncertainties and ways to fudge the theories.
LikeLiked by 1 person
Please excuse my request which only indirectly concerns the subject of your post and also my bad English as it is not my mother tongue.
Does the negative conclusion about MOND found in
Patrick M. Ogle & others, A Break in Spiral Galaxy Scaling Relations at the Upper Limit of Galaxy Mass https://doi.org/10.3847/2041-8213/ab459e
seem convincing to you?
And thank you very much for your blog and the information it brings to ignorant persons like me (because on top of everything else, I am not a scientist).
Best wishes,
Jean
LikeLike
No, I do not find this convincing. They don’t seem to be testing MOND, but rather a straw-man version thereof. MOND predicts a relation between mass and asymptotic rotation velocity. They do not appear to have measured the latter. Bright galaxies have rotation curves that decline, sometimes a lot, before flattening out. So if you measure a velocity at some intermediate radius, you will get a velocity larger than predicted. This appears to be what they did.
LikeLike
This is a bit off topic, but I noticed Dark Energy is mentioned up thread. On March 1st, Sabine posted a video interview with professor Subir Sarkar at her blog Backreaction, titled “How good is the evidence for Dark Energy?”. Professor Sarkar, and his co-authors, deduced that Dark Energy might not exist, based on their analysis of data used originally to conclude it does exist, plus, I think, more recent and larger data sets. Is there any chance you might be doing a blogpost on this reassessment of the existence of Dark Energy?
LikeLike
If Prof Sarkar is correct then you are correct. “. I was there, 3,000 internet years ago, when SCDM failed. There is nothing so sacred in ΛCDM that it can’t suffer the same fate, as has every single cosmology ever devised by humanity.”
I would very much like to read your opinion on his work.
LikeLike
I have been trying to refrain from making specific criticisms of colleagues here. I have nothing to add to the cited post: https://tritonstation.com/2019/01/28/a-personal-recollection-of-how-we-learned-to-stop-worrying-and-love-the-lambda/ – there is an enormous amount of evidence pointing to dark energy besides that which physicists obsess and argue about. It doesn’t go away if the supernova data are wrong. The question, to me, is not whether the data are right or not, but whether its interpretation as dark energy is correct. All we really know is that anything resembling a sane universe (one without dark energy), as it was conceived a few short decades ago, has been soundly falsified. The only thing we can do without breaking General Relativity is invent a substance that exerts negative pressure (dark energy). So the question is, what is really broken? Is dark energy a real entity, or a fictional entity that is convenient to cosmic calculations absent a more comprehensive theory?
LikeLike
A rather interesting new paper that proposes a Bose-Einstein Condensate of a recently discovered particle, the d-star hexaquark, as the source of dark matter has just been published: https://iopscience.iop.org/article/10.1088/1361-6471/ab67e8/pdf
One of the interesting features of this proposal is that it does predict specific decay mechanisms of the hexaquark, so is amenable to observational tests.
LikeLike
I am confused by the use of the word ‘discovered’ in reference to the d-star hexaquark. None of the articles I have looked at have specified how it was ‘discovered’. Is it something that has been seen in a particle collider experiment? If not, then it is only a theoretical particle and, to me, does not seem to deserve the attention it is getting. I would not say the Higgs Boson was ‘discovered’ until 2012 by the LHC, even though it was theorized in 1964.
Of course I am just an old amateur, so maybe the definition of ‘discovered’ has changed since I was in school?
LikeLike
Sorry. On rereading my post I think it came out a bit snarky. I did not intend it that way. I am just trying to understand what the exact status of the d-star hexaquark is.
LikeLike
Sorry.
On rereading my post it seems to have come out a bit snarky, which was not my intention.
I just wanted to know what exactly the status of the d-star hexaquark is.
I apologize for the tone of my first post.
LikeLike
I have been trying to post an apology for my earlier post.
I was unintentionally snarky, and I did not need to be.
I merely wanted to get a better understanding of the status of the d-star hexaquark.
However my apology posts seem to be getting lost, this is my third attempt.
If in fact I have posted three apologies, then I apologize for that as well.
(I am Canadian, I have a genetic need to apologize)
LikeLike
Ron,
Here is an earlier paper on the hexaquark: https://arxiv.org/pdf/1402.6844.pdf
Like all particle physics stuff, it seems pretty opaque on first reading, but if you just look at the first paragraph: “Recent exclusive and kinematically complete measurements of the basic double-pionic fusion reactions pn→dπ0π0 and pn→dπ+π− revealed a narrow resonance-like structure in the total cross section [1–3] at a mass M≈2380 MeV with a width ofΓ≈70 MeV,” it gives you the information you need.
Originally d* had been thought of as a state of six quarks in two groups of three (hence dibaryon d*), but six quarks can equally well be organised as three groups of two, which would make its mesonic nature more obvious. As a boson (even number of quarks) it can experience Bose-Einstein Condensation.
So:
1) This is a particle that does not require any extension to the Standard model
2) We know that there must have been a phase transition from the Quark-Gluon Plasma (QGP) to nucleons and this is predicted (by others) to have occurred at a temperature corresponding to an energy of ~155 MeV
3) If the BEC occurred at this time, their calculations show that the ratio of dark matter in the form of d* to baryonic matter is about what is observed.
4) There is also the possibility that the antiparticle of the d* is slightly more prone to BEC than the d*, which could explain the asymmetry between matter and antimatter, an unexplained feature of our universe.
5) It may be possible to excite individual d* out of the condensate, in which case they would have a distinctive decay signature.
This is why I described the paper as interesting. It may not be right, but any approach to DM that does not require physics beyond the Standard Model has to be interesting and is, in principle, testable with existing technology.
LikeLike
To have Standard Model particles compose the dark matter, we must prevent them from participating in Big Bang Nucleosynthesis. Maybe this paper provides a production path for d*-synthesis that satisfies this constraint, but it sounds unlikely – it’d have to be a lot more efficient, and tie-up 5/6th of the normal matter into this phase before the universe was a minute old.
No particle solution (except those contrived to do so) seems to address the real problem that galaxy dynamics imposes: everything happens *as if* MOND were the effective force-law. That’s the same “as if” Newton used in his universal law of gravity: it permits other interpretations than the obvious one. But one does have to satisfy this minimum requirement (as dipolar or superfluied dark matter do). Most particle-based hypotheses seem to be build in blissful ignorance of it, so are doomed to fail.
LikeLike
Does the CMB exist as a property of space, and is it detectable in a place as “quiet” as a dark matter lab? How hard would it be to detect it there?
LikeLike
The CMB is the redshifted radiation that is the afterglow of the Big Bang. As such, it pervades all of the empty space of the universe – which is 99.9999etc% of all space. However, it is made of ordinary photons that interact with matter when they come in contact with it. Consequently, underground laboratories are quite well-shielded from it: they don’t penetrate deep into the earth. Heck, even a tinfoil hat would suffice to block this form of cosmic radiation.
LikeLike
I don’t have a tinfoil hat. I have an aluminum one though, would that work?
😉
LikeLike
Thanks. It was not a well thought out question, but I gained a better understanding from your answer.
LikeLike
“…it means that what is driving the slope of the halo mass function is a prior that builds-in the right slope. That’s not wrong…”
Hmm, I’m not sure what you mean by not wrong. Mathematically speaking that may be acceptable, but massaging the data to produce a desired outcome can’t be considered proper science, can it?
LikeLike
Application of a prior is a necessary aspect of Bayesian statistics. The trick is to assign priors wisely. We applied the obvious prior for LCDM. The data do not have the power to reject that prior. Neither do they require it. That’s how it works. So yes, one has to interpret the results accordingly.
LikeLike
(I hope this would not be a double post – I got an error the first time while trying to post – and I didn’t save the text before hitting the Post comment button – oh well…. here I go again)
I was skimming the internet about quantized inertia and found a paper that analyses the fundamental relations of QI. I won’t give the link to the paper – maybe that was the reason for the error but here are the details: A sceptical analysis of Quantized Inertia, Michele Renda, arXiv:1908.01589.
That paper got me thinking, especially figure 3. In the paper, the author analyses the function that ties the classical inertial mass to the modified mass proposed by McCulloch without proof. What they discovered is that, unlike the initially proposed function, QI, as implied by McCulloch leads to a non-monotonic function. The function has a peak that the author says is a stable point (I’d add that only locally) – assuming a very weak force is applied to an object such that its acceleration is close to that for the peak, the interplay between the modified mass and the acceleration, given the fixed force, pulls the system towards the acceleration corresponding to the peak. For instance, if the acceleration is slightly lower that the critical acceleration, then the modified mass will tend to decrease, but since the product between the mass and the acceleration is constant (the applied force), this, in turn, will lead to an increase in the acceleration. The same reasoning can be applied if the acceleration is slightly higher that the critical acceleration.
I find this thing really interesting because it shows that sometimes the system behaviors that we think were familiar with may prove to yield surprises – who would have thought that the premises of QI as laid by McCulloch lead to such a non-monotonic function? (For the record, I’m not convinced by QI, or at least not by how McCulloch presents it).
But that graph made me wonder why the interpolation function in MoND needs to be monotonic – are there hard constraints for this in all regimes?
I would assume that in the classical regime and down to about a0 the function should be monotonic. But what prevents it for the deep MoND regime to have peaks and / or valleys (a la Chebyshev filter response) before settling to u(a/a0) = a/a0?
What would be the impact of this for galaxy clusters? How could this be tested / ruled out?
As a note, what immediately drew my attention initially was the value of the critical acceleration which I tied it (incorrectly) to MoND – they found 1.2e-9 m/s^2. This value is 10 times higher than a0 and this lead me to think about the monotonic assumption for the interpolation function
LikeLike
There is, so far, no hint in galaxy data to any ringing or sharp transition in the interpolation function, the shape of which is empirically traced the the radial acceleration relation (https://tritonstation.com/2016/09/26/the-third-law-of-galactic-rotation/). Modern data show a pretty gradual transition with no ringing in either asymptotic limit – at least at the level we can currently perceive. Data of other types are less clear, so one can more readily imagine such behavior in clusters or cosmology. Indeed, Bekenstein’s TeVeS envisioned a separate cosmic function. So I’m sure there is room to play in theory space, but there isn’t really any empirical indication of a non-monotonic interpolation function.
LikeLike