I recently traveled to my first international meeting since the Covid pandemic began. It was good to be out in the world again. It also served as an excellent reminder of the importance of in-person interactions. On-line interactions are not an adequate substitute. I’d like to be able to recount all that I learned there, but it is too much. This post will touch on one of the much-discussed topics, our own Milky Way Galaxy.
When I put on a MOND hat, there are a few observations that puzzle me. The most persistent of these include the residual mass discrepancy in clusters, the cosmic microwave background, and the vertical motions of stars in the Milky Way disk. Though much hyped, the case for galaxies lacking dark matter does not concern me much: the examples I’ve seen so far appear to be part of the normal churn of early results that are likely to regress toward the norm as the data improve. I’ve seen this movie literally hundreds of times. I’m more interested in understanding the forest than a few outlying trees.
The Milky Way is a normal galaxy – it is part of the forest. It is easy to get lost in the leaves when one has access to data for millions going on billions of individual stars. These add up to a normal spiral galaxy, and we know a lot about external spirals that can help inform our picture of our own home.
For example, by assuming that the Milky Way falls along the radial acceleration relation defined by other spiral galaxies, I was able to build a mass model of its surface density profile. The resulting mass distribution is considerably more detailed than the usual approach of assuming a smooth exponential disk, which would be a straight line in the right-hand plot below. With the level of detail becoming available from missions like the Gaia satellite, it is necessary to move beyond such approximations.

This model was built before Gaia data became available, and is not informed by it. Rather, I took the terminal velocities measured by McClure-Griffiths & Dickey, which provide the estimate of the Milky Way rotation curve that is most directly comparable to what we measure in external spirals, and worked out the surface density profile using the radial acceleration relation. The resulting model possesses bumps and wiggles like those we see corresponding to spiral arms in external galaxies. And indeed, it turns out that the locations of these features correspond with known spiral arms. Those are independent observations: one is from the kinematics of interstellar gas, the other from traditional star counts.
The model turns out to have a few further virtues. It matches the enclosed mass profile of the inner bulge/bar region of the Galaxy without any attempt at a specific fit. It reconciles the rotation curve measured with stars using Gaia data with that measured using gas in the interstellar medium – a subtle difference that was nevertheless highly significant. It successfully predicts that the rotation curve beyond the solar radius would not be perfectly flat, but rather decline at a specific rate – and exactly that rate was subsequently measured using Gaia. These are the sort of results that inclines one to believe that the underlying physics has to be MOND. Inferring maps of the mass distribution with this level of detail is simply not possible using a dark matter model.

Great, right? It is. It also makes a further prediction: we can use the mass model to predict the vertical motions of stars perpendicular to the Milky Way’s disk.
Most of the kinetic energy of stars orbiting in the solar neighborhood is invested in circular motion: the vast majority of stars are orbiting in the same direction in the same plane at nearly the same speed. There is some scatter, of course, but radial motions due to orbital eccentricities represent a small portion of the kinetic energy budget. As stars go round and round, the also bob up and down, oscillating perpendicular to the plane of the disk. The energy invested in these vertical motions is also small, which is why the disk of the Milky Way is thin.

Knowing the surface density profile of the Milky Way disk, we can predict the vertical motions. In the context of dark matter, most of the restoring force that keeps stars near the central plane is provided by the stars themselves – the dark matter halo is quasi-spherical, and doesn’t contribute much to the restoring force of the disk. In MOND, the stars and gas are all there is. So the prediction is straightforward (if technically fraught) in both paradigms. Here is a comparison of both predictions with data from Bovy & Rix (2013).
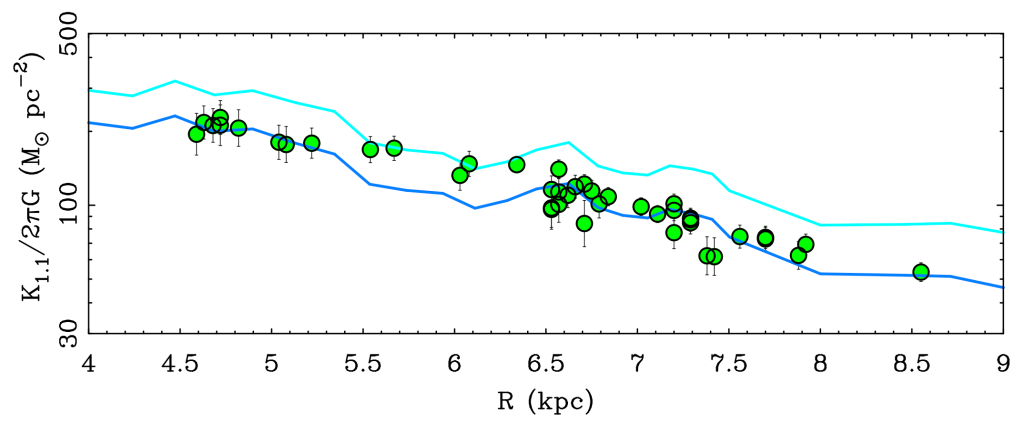
Looks great again, right? The dark blue line goes right through the data with zero fitting. The only exception is in the radial range 5.5 to 6.4 kpc, which turns out to be where the stars probing the vertical motion are maximally different from the gas informing the prediction: we’re looking at different Galactic longitudes, right where there is or is not a spiral arm, so perhaps we should get a different answer in this range. Theory gives us the right answer, no muss, no fuss.
Except, hang on – the line that fits is the Newtonian prediction. The prediction of MOND overshoots the data. It gets the shape right, but the naive MOND prediction is for more vertical motion than we see.
By the “naive” MOND prediction, I mean that we assume that MOND gives the same boost in the vertical direction as it does in the radial direction. This is the obvious first thing to try, but it is not necessarily what happens in all possible MOND theories. Indeed, there are some flavors of modified inertia in which it should not. However, one would expect some boost, and in these data there appears to be none. We get the right answer with just Newton and stars. There’s not even room for much dark matter.
I hope Gaia helps us sort this out. I worry that it will provide so much information that we risk missing the big picture for all the leaves.
This leaves us in a weird predicament. The radial force is extraordinarily well-described by MOND, which reveals details that we could never hope to access if all we know about is dark matter. But if we spot Newtonian gravity this non-Newtonian information from the radial motion, it predicts the correct vertical motion. It’s like we have MOND in one direction and Newton in another.
This makes no sense, so is one of the things that worries me most about MOND. It is not encouraging for dark matter either – we don’t get to spot ourselves MOND in the radial direction then pretend that dark matter did it. At present, it feels like we are up the proverbial creek without a paddle.
I seems to me the result follows from the geometry. The radial forces of the disk fall off as 1/r because they lie along the flat disk, a circular geometry. The vertical forces, lying orthogonal to the disk implicate a spherical geometry with a 1/r^2 drop off. No?
LikeLike
The way I thought about it is if you have an infinitely extended uniform horizontal thin disk and use Newton’s Law, then the gravitational force in the vertical direction on a star above the disk is constant, regardless of the star’s distance (r) from the disk plane, because if you take a cone centred on the star the area of the disk intersected by it scales as r^2 so exactly corrects for the reduction in gravitational force with distance. So, for a finite disk, it is only when the star is infinitely far from it (or at least at a large distance compared with the disk diameter) that you expect a 1/r^2 drop off.
In practice, the disk is non-uniform, because its density reduces as a function of distance from the galactic centre, but for stars that are close to the disk, compared with the disk size, this may not be a bad first approximation.
LikeLike
Yes, the infinite slab is a common approximation in this problem. Seems like it should be good enough, at least for the traditional Oort problem, since the solar circle is a tiny patch of a giant Milky Way. But we’re getting beyond the tiny patch, so both the geometry of the disk and the density fluctuations (like spiral arms) within it start to matter.
LikeLike
Dear Stacy,
Rather than “up the proverbial creek without a paddle”, I found this blog post fascinating and inspiring. If such phenomenology holds up under more data, i.e., that MOND and a_0 are essentially coupled only to the centripetal part of acceleration, but not to the d^2 r/dt^2 (nor d^z/dt^2 for cylindrical), this would be big news — either a crucial new tenet in MOND or, at least, an essential modification of the 3rd tenet limiting it to centripetal accelerations. (As a consequence, the theoretical computations of weak lensing in MOND, may also be affected, no?)
I eagerly await a more detailed paper. (?)
Best wishes.
LikeLike
It could be telling us something about the underlying theory, yes. I hope, in my copious spare time, to see if this can be used to constrain the nonlocality of the modified inertia theory Milgrom suggested. There is a lot to sort out in the data though: what I show here is certainly not the last word, and will be completely replaced by Gaia data in the coming years.
LikeLike
Differing radial and orthogonal acceleration profiles would indicate a non-Newtonian stress/energy tensor, right? ∴ TOV equation not applicable.
LikeLike
Where is the last figure from? I didn’t find it in Bovy & Rix (2013).
LikeLike
The data are from Bovy & Rix. The figure is based on a figure in my 2016 paper. I’ve added the MOND line, which I didn’t include there because (i) that was not a MOND paper, and (ii) I didn’t understand it. I still don’t.
LikeLike
I left a lot unsaid in this post as it was going to take several weeks to write 10,000+ words about it all. One detail is that there can be vertical structure as well as radial structure. Allowing for radial structure – the bumps and wiggles – reduces the chi^2 of the fit to the rotation curve from 14 (unacceptable) to around 1 (a good fit). [See Fig. 1 and Table 1 of my 2019 paper; also http://astroweb.case.edu/ssm/models/MWaddenda2015.html ]. Which is to say, we have to get past the usual exponential approximation.
If that’s true in the radial direction, it may also be true in the vertical direction. At some level, we already know this to be the case: the main stellar disk is thin, but there is also a thick disk. In MOND, one also needs to worry about the gas disk, which usually gets ignored in conventional analyses. So, even using the exponential approximation, we have at least 3 distinct components, each with their own scale height. There are indications that the exponential approximation is too sharp in that it is more concentrated at z=0 than the data. There are other functional forms (sech^2 is popular), but reality may probably doesn’t look like any nice smooth function when we look hard enough. So the difficulty in fitting the vertical motions may in part be an indication that structure in the disk matters in the vertical direction just as it matters in the radial direction.
LikeLiked by 3 people
Very interesting topic! The notion of vertical structure accounting for the directional difference doesn’t sit too well with me though, for the simple fact that you pointed to a fairly accurate fit to the shape for the Newtonian model.
What would you say are the experimental differences in which the radial and vertical component acceleration measurements are being made?
LikeLike
I have a question, and hopefully you can answer it. Naïvely, I would think that our knowledge of the expected gravitational potential in our region of the milky way is more accurate than the actual, measured value. That is, it’s easier to measure the position and distance of stars, and density of gaz, which allows us to calculate a potential, than to measure the 3-vector of stars and gaz clouds telling us about the actual value of the potential where the star/cloud is.
That is to say, it’s easier to accurately draw the line of the Newtonian and MOND expectations on your last figure than to put data on it. Until we can analyze the latest release of Gaia data anyway (and even then I expect we could extend the region where position and distance are still well known, but I’m no expert).
Does it make sense? I’m trying to figure out how discriminating the difference between the two predictions is. If we have a solid difference, and eventually data aligns with one of the two lines, that would be a revolution. A revolution for supporters of dark matter if the best fit is the MOND expectation (that should seriously shake them, if nothing else does), and a revolution for supporters of MOND otherwise.
LikeLike
In principle, yes, but in practice, this is astronomy. Much of the stellar mass is in low mass stars that are difficult to see more than a few tens of parsecs away. So we usually assume they come in proportion to the more readily visible stars. This seems to be a good assumption when averaged over a whole galaxy, but it may break down on smaller scales.
LikeLike
Thank you. It makes so much sense, yet i’d never have thought about that.
LikeLike
On a different topic, I like the new banner. Much nicer than the old one. 🙂
LikeLiked by 1 person
It seems that there’s no theory that works in more than one complexity hierarchical level.
Quantum Mechanics is only good in simple quantum assemblies, it will be an exercise in futility trying to use quantum Mechanics to predict the behavior of living beings, even more using it to model ecosystems.
“General” Relativity works in simple gravitational assemblies as the solar system but fails at galaxy level complexity.
MOND seems to work for galaxy level complexity but fails at galaxy cluster complexity.
Reality hierarchical structures are a strong indication that higher hierarchical structures are “decoupled” from the dynamics governing their elementary components subjected to higher energy densities, this is true for quantum mechanical assemblies(see Decoupling theorems for effective field theories) and it seems to be true for gravitational assemblies, perhaps some kind of decoupling theorem holds true in that context.
LikeLike
Certainly all our theories are at best approximations of reality. I’m old enough to remember when people started fantasizing about theories of everything, and here we are.
LikeLike
But precisely ignoring this basic fact (naive reductionism) is the root of many problems: trying to use a single theory in different hierarchical structures, basically ignoring the obvious hierarchical structure, like using organic chemistry to model social behavior.
LikeLike
What hierarchies are present in this post — it seems to be entirely about galaxy-level dynamics, the precise realm where you suggest MOND works, and yet naive MOND doesn’t appear to work.
LikeLike
I am referring indirectly to the adhoc introduction of dark matter when general Relativity failed to explain galaxies “rigid” rotational speed: galaxy level hierarchical is a level above simple gravitational systems as the solar system; or claiming that MOND is wrong because it appears to fail at galaxy cluster hierarchical level, that is a level above galaxy where it was developed initially, it’s doubtful that it will ever work at that level.
Again: theories seem to work only at one hierarchical level, and that it’s actually expected as Reality hierarchical structures are a reflection of the underlying properties/dynamics.
More is different, the total is more than the sum of it’s parts, with enough quantity new qualities may arise… Complexity is a source of irreducibility.
Not by chance P. Anderson was hated by the naive reductionist cultists, the people talking about a theory of everything, or “Dreams of a final theory”(Steven Weinberg).
Dogmatism, the Achilles heel of theoreticians, ultimately negates objectivity.
LikeLike
could Gravitational force distribution in fractal structures explain MOND in one direction and Newton in another
https://www.researchgate.net/publication/1840875_Gravitational_force_distribution_in_fractal_structures
are there any analogies with magnetic spinning disks ( MOND in one direction and Newton in another )
LikeLike
Certainly the distribution of matter is important.
LikeLike
. We get the right answer with just Newton and stars. There’s not even room for much dark matter.
does this falsify dark matter theories ?
LikeLike
Dear Stacy,
I hope you will be able to come to my talk in St Andrews in June, in which I plan to try to explain why MOND is directional in the way that these data imply.
LikeLike
I will be there.
LikeLike
Oh my, I wish I could be there too. I hope you will post some summary…
LikeLike
I hope I haven’t promised more than I can deliver, as I’m still working out details. The basic ideas go back several years, but getting actual equations down on paper has proved tricky. My approach is to ask, what would Hamilton say about MOND? I have become more and more convinced that he would say “I told you so!” – the unwanted cross-terms that quaternions introduced into the physical equations, and that caused quaternions to be written out of physics, seem to be exactly the extra terms that MOND requires. By quantising a quaternionic inertial/gravitational mass using a variation of arXiv:2205.13390 I get the directionality into MOND as well.
LikeLike
> I plan to try to explain why MOND is directional > in the way that these data imply
Is a preprint available somewhere?
LikeLike
I’m afraid not. The arXiv didn’t like it, probably because I claimed that MOND can explain the proton/neutron mass ratio to an accuracy of 10ppm, which is clearly an absurd claim! So I’m trying to re-write it to explain in detail how the Schroedinger equation is affected by MOND. In the meantime, there are some brief descriptions on my blog, though full of inaccuracies and exaggerations, I am sure.
LikeLike
There is, perhaps, a “simple” explanation as to why the dynamic would be “more” Newtonian along the z-axis.
In the Milky Way, on the galactic plane, the region where MOND effects dominate lies at the edge, and there in the reference frame of, say, a star, most of the gravitational pull comes from the center of the galaxy. When I say most I mean it comes essentially from a direction that appears to be a line extending a few dozens of degrees in the general direction of the galactic center, approximately.
Not so much along the z-axis where the pull comes from a plane that covers almost half the sky. Now, if we assume that these sources cancel each other because they are of the same strength and come from almost opposite directions, we can use the infinite-disk approximation and the local gravitational field strength is much lower than if there was no cancelation (ignoring the fact that, on the contrary, near the star the field quite strong, but that’s a different problem).
Now the MOND effect kicks in when the strength of the gravitational field is low (below the infamous a0 constant), but I believe that this is also assuming different fields cancel each other. That is, if instead we were calculating the sum of all contributions as scalars rather than vectors, the situation would be very different!
For example there is a review of MOND (“From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity” section 11.5.1) in which the authors describe how MOND could be tested near Saturn, where all gravitational fields — the Galaxy, the Sun and planets — cancel each other in a small region of space. It obviously assumes this cancelation works for MOND. If it wasn’t, testing MOND within the solar system would be pretty much impossible.
So what I’m saying is that perhaps when we analyze MOND effects in the Milky Way along the z-axis, that’s what we are seeing : fields coming from opposite directions don’t cancel each other that much. We should then expect to encounter MONDian dynamic only at much higher values of ‘z’. This is extremely interesting!
LikeLike
That the vertical acceleration of stars in the outer disc follows Newton, and not MOND is a feature of galactic dynamics I never considered in a home-brewed, quite amateur hypothesis that I cooked up some time ago. But being in the recovery stage of a wicked bad case of Covid I’m hardly in a state of mind to think deeply, unfortunately.
LikeLike
Huh, so maybe some weird directional thing? Isn’t that like the dismissed electro-gravitational theory of GR? (I’m screwing up the right name.) You should totally be on the Lex Fridman podcast.
LikeLike
I’m wondering if Deur’s theory predicts vertical Newtonian gravity (no self interaction addition vertically) for spiral galaxies. It’s too complicated for me to say for sure, still I have the feeling that’s what it predicts.
LikeLike
According to Anthony Lasenby et al, the effects of gravitational confinement in Alexandre Deur’s theory are actually too small to predict any significant deviations from Newtonian gravity/GR:
https://arxiv.org/abs/2303.11094
https://arxiv.org/abs/2303.06115
LikeLike
The impact of this paper on Deur’s work is extensively discussed at the physics forum thread titled: “Deur Gravitational Self-interaction Doesn’t Explain Galaxy Rotation Curves”. I’m not sure I can link to it but here goes: https://www.physicsforums.com/threads/deur-gravitational-self-interaction-doesnt-explain-galaxy-rotation-curves.1050848/
LikeLike
This discovery of the directional dependence of MOND behavior is very interesting. Maybe it is related to whether or not there is an underlying identifiable gradient in time that can affect the frequency of the light being measured. In other words, maybe MOND is a measurement effect influenced by a time-like field.
LikeLike
The alcubierre metric is different in AeST 🙂 I made a few simulations today, I’m now a lot more excited for this theory
LikeLiked by 1 person
Great as it is, MOND was never going to be the final word on gravity. It is a useful stepping stone to the solution. In my opinion self interacting gravity is more promising and doesn’t suffer this problem.
LikeLike